题目内容
（2013•和平区二模）在△ABC中，A=
，cosB=
．
（I）求cos C；
（II）设BC=
，求AC和AB．
| π |
| 4 |
| ||
| 5 |
（I）求cos C；
（II）设BC=
| 5 |
分析：（I）根据cosB=
，利用同角三角函数的基本关系算出sinB=
=
．由诱导公式得cosC=-cos（A+B），结合两角和的余弦公式展开，代入数据即可得到cos C的值；
（II）根据正弦定理，结合题中数据算出AC=
=2
．然后利用余弦定理，算出AB2=AC2+BC2-2AC•BCcosC=9，即可得到AB=3．
| ||
| 5 |
| 1-cos2B |
2
| ||
| 5 |
（II）根据正弦定理，结合题中数据算出AC=
| BC•sinB |
| sinA |
| 2 |
解答：解：（I）∵cosB=
＞0，B∈（0，π）
∴B为锐角，且sinB=
=
∵A+B=π-C，
∴cosC=-cos（A+B）=sinAsinB-cosAcosB=
×
-
×
=
；
（II）根据正弦定理，得
=
∴AC=
=
=2
由余弦定理，得AB2=AC2+BC2-2AC•BCcosC=8+5-2×2
×
×
=9
∴AB=3（舍负）
| ||
| 5 |
∴B为锐角，且sinB=
| 1-cos2B |
2
| ||
| 5 |
∵A+B=π-C，
∴cosC=-cos（A+B）=sinAsinB-cosAcosB=
| ||
| 2 |
2
| ||
| 5 |
| ||
| 2 |
| ||
| 5 |
| ||
| 10 |
（II）根据正弦定理，得
| AC |
| sinB |
| BC |
| sinA |
∴AC=
| BC•sinB |
| sinA |
| ||||||
|
| 2 |
由余弦定理，得AB2=AC2+BC2-2AC•BCcosC=8+5-2×2
| 2 |
| 5 |
| ||
| 10 |
∴AB=3（舍负）
点评：本题给出△ABC的两个角，求第三个角的余弦并在已知BC边的情况下求另外两条边长．着重考查了诱导公式、两角和的余弦公式和正余弦定理等知识，属于中档题．
练习册系列答案
相关题目
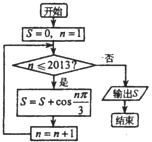（2013•和平区二模）阅读如图所示的程序框图，运行相应的程序，则输出的结果S的值为（ ）
（2013•和平区二模）已知函数y=Asin（ωx+φ）（A＞0，ω＞0），|φ|＜π）的部分图象如图所示，则它的解析式为（ ）