题目内容
13.已知a,b,x,y∈R+,且$\frac{a}{x}$+$\frac{b}{y}$=1,求x+y的最小值.分析 整体代入可得x+y=($\frac{a}{x}$+$\frac{b}{y}$)(x+y)=a+b+$\frac{ay}{x}$+$\frac{bx}{y}$,由基本不等式可得.
解答 解:∵a,b,x,y∈R+,且$\frac{a}{x}$+$\frac{b}{y}$=1,
∴x+y=($\frac{a}{x}$+$\frac{b}{y}$)(x+y)=a+b+$\frac{ay}{x}$+$\frac{bx}{y}$
≥a+b+2$\sqrt{\frac{ay}{x}•\frac{bx}{y}}$=a+b+2$\sqrt{ab}$=$(\sqrt{a}+\sqrt{b})^{2}$
当且仅当$\frac{ay}{x}$=$\frac{bx}{y}$时取等号,
联立$\frac{a}{x}$+$\frac{b}{y}$=1和$\frac{ay}{x}$=$\frac{bx}{y}$可得x=a+$\sqrt{\frac{a}{b}}$且y=$\sqrt{ab}$+1时,x+y取最小值$(\sqrt{a}+\sqrt{b})^{2}$
点评 本题考查基本不等式求最值,整体代入化为可用基本不等式的形式是解决问题的关键,属基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 如图,在正方体ABCD-A1B1C1D1中,M,N分别是CD,CC1的中点,给出下列命题:
如图,在正方体ABCD-A1B1C1D1中,M,N分别是CD,CC1的中点,给出下列命题: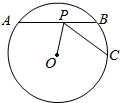 如图,点P为⊙O的弦AB上一点,且AP=9,BP=4,连接OP,作PC⊥OP交圆于C,则PC的长为( )
如图,点P为⊙O的弦AB上一点,且AP=9,BP=4,连接OP,作PC⊥OP交圆于C,则PC的长为( )