题目内容
已知等差数列{an} 的前n项和为Sn,a2=9,S5=65.
(I)求{an} 的通项公式:
(II)令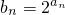 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
解:(I) (2分)
(2分)
解得: (4分),
(4分),
所以an=4n+1(6分)
(II)由(I)知 (7分)
(7分)
因为 ,(8分)
,(8分)
所以{bn} 是首项为b1=32,公比q=16的等比数列(9分),
所以 .(12分)
.(12分)
分析:(I)利用等差数列的首项a1及公差d表示已知条件,解出a1,d代入等差数列的通项公式可求
(II)由(I)可求 ,从而可得数列{bn} 是首项为b1=32,公比q=16的等比数列,代入等比数列的前n项和公式可求
,从而可得数列{bn} 是首项为b1=32,公比q=16的等比数列,代入等比数列的前n项和公式可求
点评:在数列的基本量的求解中要求考生熟练掌握基本公式,具备一定的计算能力,本题属于基础试题.
 (2分)
(2分)解得:
 (4分),
(4分),所以an=4n+1(6分)
(II)由(I)知
 (7分)
(7分)因为
 ,(8分)
,(8分)所以{bn} 是首项为b1=32,公比q=16的等比数列(9分),
所以
 .(12分)
.(12分)分析:(I)利用等差数列的首项a1及公差d表示已知条件,解出a1,d代入等差数列的通项公式可求
(II)由(I)可求
 ,从而可得数列{bn} 是首项为b1=32,公比q=16的等比数列,代入等比数列的前n项和公式可求
,从而可得数列{bn} 是首项为b1=32,公比q=16的等比数列,代入等比数列的前n项和公式可求点评:在数列的基本量的求解中要求考生熟练掌握基本公式,具备一定的计算能力,本题属于基础试题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.