题目内容
已知函数f(x)=ax(a∈R),g(x)=lnx-1.
(1)若函数h(x)=g(x)+1- f(x)-2x存在单调递减区间,求a的取值范围;
f(x)-2x存在单调递减区间,求a的取值范围;
(2)当a>0时,试讨论这两个函数图象的交点个数.
解:(1)h(x)=lnx-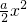 -2x(x>0),
-2x(x>0),
h′(x)= -ax-2.
-ax-2.
若使h(x)存在单调递减区间,则h′(x)= -ax-2<0在(0,+∞)上有解.
-ax-2<0在(0,+∞)上有解.
而当x>0时, -ax-2<0?ax>
-ax-2<0?ax> -2?a>
-2?a> -
- 问题转化为
问题转化为
a>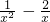 在(0,+∞)上有解,故a大于函数
在(0,+∞)上有解,故a大于函数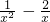 在(0,+∞)上的最小值.
在(0,+∞)上的最小值.
又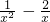 =
=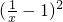 -1,
-1,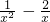 在(0,+∞)上的最小值为-1,所以a>-1.
在(0,+∞)上的最小值为-1,所以a>-1.
(2)令F(x)=f(x)-g(x)=ax-lnx+1(a>0)
函数f(x)=ax与g(x)=lnx-1的交点个数即为函数F(x)的零点的个数.
F′(x)=a- (x>0)
(x>0)
令F(x)=a- =0解得x=
=0解得x= .
.
随着x的变化,F(x),F(x)的变化情况如表:
 (7分)
(7分)
①当F( )=2+lna>0,即a=e-2时,F(x)恒大于0,函数F(x)无零点.(8分)
)=2+lna>0,即a=e-2时,F(x)恒大于0,函数F(x)无零点.(8分)
②当F( )=2+lna=0,即a=e-2时,由上表,函数F(x)有且仅有一个零点.
)=2+lna=0,即a=e-2时,由上表,函数F(x)有且仅有一个零点.
③F( )=2+lna<0,即0<a<e-2时,显然1<
)=2+lna<0,即0<a<e-2时,显然1<
F(1)=a+1>0,所以F(1)F( )<0•,
)<0•,
又F(x)在(0, )内单调递减,
)内单调递减,
所以F(x)在(0, )内有且仅有一个零点
)内有且仅有一个零点
当x> 时,F(x)=ln
时,F(x)=ln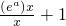
由指数函数y=(ea)x(ea>1)与幂函数y=x增长速度的快慢,知存在x0>
使得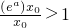 从而F(x0)=ln
从而F(x0)=ln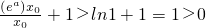
因而F( )•F(x0<0)
)•F(x0<0)
又F(x)在( ,+∞)内单调递增,
,+∞)内单调递增,
F(x)在[ ,+∞)上的图象是连续不断的曲线,
,+∞)上的图象是连续不断的曲线,
所以F(x)在( ,+∞)内有且仅有一个零点.
,+∞)内有且仅有一个零点.
因此,0<a<e-2时,F(x)有且仅有两个零点.
综上,a>e-2,f(x)与g(x)的图象无交点;
当a=e-2时,f(x)与g(x)的图象有且仅有一个交点;
0<a<e-2时,f(x)与g(x)的图象有且仅有两个交点.
分析:(1)先求出函数h′(x),欲使h(x)存在单调递减区间,则h′(x)<0在(0,+∞)上有解,然后利用分离法可得a>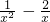 在(0,+∞)上有解,故a大于函数
在(0,+∞)上有解,故a大于函数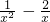 在(0,+∞)上的最小值即可.
在(0,+∞)上的最小值即可.
(2)先令F(x)=f(x)-g(x)=ax-lnx+1(a>0),函数f(x)=ax与g(x)=lnx-1的交点个数即为函数F(x)的零点的个数,利用导数研究函数F(x)的最小值,比较最小值与0的大小即可得到F(x)的零点的个数.
点评:本题主要考查了利用导数研究函数的单调性,函数的零点与方程根的关系等基础题知识,考查了转化和划归的数学思想,属于中档题.
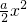 -2x(x>0),
-2x(x>0),h′(x)=
 -ax-2.
-ax-2.若使h(x)存在单调递减区间,则h′(x)=
 -ax-2<0在(0,+∞)上有解.
-ax-2<0在(0,+∞)上有解.而当x>0时,
 -ax-2<0?ax>
-ax-2<0?ax> -2?a>
-2?a> -
- 问题转化为
问题转化为a>
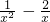 在(0,+∞)上有解,故a大于函数
在(0,+∞)上有解,故a大于函数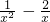 在(0,+∞)上的最小值.
在(0,+∞)上的最小值.又
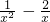 =
=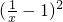 -1,
-1,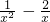 在(0,+∞)上的最小值为-1,所以a>-1.
在(0,+∞)上的最小值为-1,所以a>-1.(2)令F(x)=f(x)-g(x)=ax-lnx+1(a>0)
函数f(x)=ax与g(x)=lnx-1的交点个数即为函数F(x)的零点的个数.
F′(x)=a-
 (x>0)
(x>0)令F(x)=a-
 =0解得x=
=0解得x= .
.随着x的变化,F(x),F(x)的变化情况如表:
 (7分)
(7分)①当F(
 )=2+lna>0,即a=e-2时,F(x)恒大于0,函数F(x)无零点.(8分)
)=2+lna>0,即a=e-2时,F(x)恒大于0,函数F(x)无零点.(8分)②当F(
 )=2+lna=0,即a=e-2时,由上表,函数F(x)有且仅有一个零点.
)=2+lna=0,即a=e-2时,由上表,函数F(x)有且仅有一个零点.③F(
 )=2+lna<0,即0<a<e-2时,显然1<
)=2+lna<0,即0<a<e-2时,显然1<
F(1)=a+1>0,所以F(1)F(
 )<0•,
)<0•,又F(x)在(0,
 )内单调递减,
)内单调递减,所以F(x)在(0,
 )内有且仅有一个零点
)内有且仅有一个零点当x>
 时,F(x)=ln
时,F(x)=ln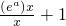
由指数函数y=(ea)x(ea>1)与幂函数y=x增长速度的快慢,知存在x0>

使得
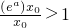 从而F(x0)=ln
从而F(x0)=ln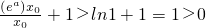
因而F(
 )•F(x0<0)
)•F(x0<0)又F(x)在(
 ,+∞)内单调递增,
,+∞)内单调递增,F(x)在[
 ,+∞)上的图象是连续不断的曲线,
,+∞)上的图象是连续不断的曲线,所以F(x)在(
 ,+∞)内有且仅有一个零点.
,+∞)内有且仅有一个零点.因此,0<a<e-2时,F(x)有且仅有两个零点.
综上,a>e-2,f(x)与g(x)的图象无交点;
当a=e-2时,f(x)与g(x)的图象有且仅有一个交点;
0<a<e-2时,f(x)与g(x)的图象有且仅有两个交点.
分析:(1)先求出函数h′(x),欲使h(x)存在单调递减区间,则h′(x)<0在(0,+∞)上有解,然后利用分离法可得a>
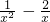 在(0,+∞)上有解,故a大于函数
在(0,+∞)上有解,故a大于函数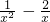 在(0,+∞)上的最小值即可.
在(0,+∞)上的最小值即可.(2)先令F(x)=f(x)-g(x)=ax-lnx+1(a>0),函数f(x)=ax与g(x)=lnx-1的交点个数即为函数F(x)的零点的个数,利用导数研究函数F(x)的最小值,比较最小值与0的大小即可得到F(x)的零点的个数.
点评:本题主要考查了利用导数研究函数的单调性,函数的零点与方程根的关系等基础题知识,考查了转化和划归的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目