题目内容
设直线l1和l2相交于点R,l1⊥l2,M、N∈l1,|MN|=4,M分| RN |
| 5 |
| 4 |
B2,p1、p2分别是A1B1和A2B2的中点,且A1B1⊥A2B2.
(1)求曲线C的方程;
(2)求点p1和p2到直线l1距离的乘积.
分析:(1)先以l1为x轴,过M且垂直于l1的直线为y的轴,建立直角坐标系根据题意可求得曲线的方程.
(2)由(1)可设A1,B1,A2,B2的坐标,即研究A1B1和A2B2的中点纵坐标绝对值之积.
(2)由(1)可设A1,B1,A2,B2的坐标,即研究A1B1和A2B2的中点纵坐标绝对值之积.
解答:解:(1)以l1为x轴,过M且垂直于l1的直线为y的轴,
建立直角坐标系,点M为坐标原点,此时,
点N的坐标为(4,0),直线l2的方程为x+5=0.
由题意可知.曲线方程是y2=16x.
(2)设A1,B1,A2,B2的坐标依次为:
(
,y1),(
,y2),(
,y3),(
,y4).
若y12=y22,由于A1,B1是不同点,
∴y1=-y2≠0,
∴AB⊥x轴,从而A2B2∥x轴.
由于平行于x轴的直线与抛物线只能有一个交点矛盾,
∴y12≠y22,
同理y32≠y42,
A1B1斜率为
,
A2B2的斜率为
.
由于A1B1⊥A2B2
得(y1+y2)(y3+y4)=-162.
因P1,P2的纵坐标分别为
,
,
∴它们的乘积为(
)(
)=-64,
点P1和P2到直线l1的距离的乘积为64.
建立直角坐标系,点M为坐标原点,此时,
点N的坐标为(4,0),直线l2的方程为x+5=0.
由题意可知.曲线方程是y2=16x.
(2)设A1,B1,A2,B2的坐标依次为:
(
| y12 |
| 16 |
| y22 |
| 16 |
| y32 |
| 16 |
| y43 |
| 16 |
若y12=y22,由于A1,B1是不同点,
∴y1=-y2≠0,
∴AB⊥x轴,从而A2B2∥x轴.
由于平行于x轴的直线与抛物线只能有一个交点矛盾,
∴y12≠y22,
同理y32≠y42,
A1B1斜率为
| 16 |
| y1+y2 |
A2B2的斜率为
| 16 |
| y3 +y4 |
由于A1B1⊥A2B2
得(y1+y2)(y3+y4)=-162.
因P1,P2的纵坐标分别为
| y1+ y2 |
| 2 |
| y3+y4 |
| 2 |
∴它们的乘积为(
| y1+ y2 |
| 2 |
| y3+y4 |
| 2 |
点P1和P2到直线l1的距离的乘积为64.
点评:本师主要考查直角坐标系的建立及曲线方程的求法和应用.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=4.
在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=4.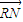 所成比为
所成比为 ,记到点N的距离比它到直线l2的距离小1的点的轨迹为曲线C,在曲线C上取点A1,B1,A2
,记到点N的距离比它到直线l2的距离小1的点的轨迹为曲线C,在曲线C上取点A1,B1,A2