Question

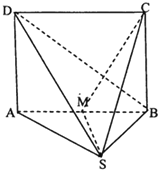（2013•保定一模）四棱锥S-ABCD中，四边形ABCD为矩形，M为AB中点，且△SAB为等腰直角三角形，SA=SB=2，SC⊥BD，DA⊥平面SAB．
（1）求证：平面SBD⊥平面SMC
（2）设四棱锥S-ABCD外接球的球心为H，求棱锥H-MSC的高；
（3）求平面SAD与平面SMC所成的二面角的正弦值．

Answer 1

分析：（1）结合已知条件，由线面垂直的判定定理证出SM垂直于平面ABCD，从而得到SM垂直于DB，由已知SC垂直于BD，得到DB垂直于SMC，利用面面垂直的判定定理得到要证的结论；
（2）连结AC、BD交于N，通过证明SB垂直于SD说明N即为四棱锥S-ABCD外接球的球心为H，结合（1）可知CM与BD的交点Q即为H在平面SMC上的射影，通过解三角形即可得到HQ的长度；
（3）以M为坐标原点建立空间直角坐标系，通过求解平面SAD与平面SMC法向量所成角的余弦值得到平面SAD与平面SMC所成的二面角的正弦值．

解答：（1）证明：如图，
∵SA=SB，M为AB的中点，∴SM⊥AB，
又∵DA⊥平面SAB，∴DA⊥SM，
所以，SM⊥平面ABCD．
又∵DB?平面ABCD，∴SM⊥DB．
又∵SC⊥BD，∴DB⊥平面SMC，
∴平面⊥平面SMC；
（2）解：由（1）知DB⊥平面SMC，∴DB⊥MC．
∴△ABD∽△BCM，故

AB

AC

=

DA

MB

⇒

2 2

BC

=

BC

2

⇒BC=2
设AC∩BD=N，∵AS⊥BS，DA⊥BS，
∴SB⊥平面SAD．
∴SB⊥SD．
所以NA=NB=NC=ND=NS，∴H与N重合，即为球心．
设MC∩DB=Q，由于DB⊥平面SMC，故HQ即为所求．
∵MC=

22+( 2 )2

=

6

．
∴QB=

BC•MB

MC

=

2 2

6

=

2 3

3

．
∵BD=

22+(2 2 )2

=2

3

，∴HB=

3

．
故HQ=

3

-

2

3

3

=

3

3

．
即棱锥H-MSC的高为

3

3

；
（3）解：以点M为原点，建立坐标系如图，
则M（0，0，0），S（

2

，0，0），C（0，

2

，2），D（0，-

2

，2）．
∴

MS

=(

2

，0，0)，

MC

=（0，

2

，2），

AD

=(0，0，2)，

AS

=(

2

，

2

，0)．
设平面SMC的法向量为

n

=(x，y，z)，ASD的法向量为

m

=(a，b，c)
由

n • MS =0 n • MC =0

，得

2 x=0 2 y+2z=0

，取z=-1，得x=0，y=

2

．
所以

n

=(0，

2

，-1)．
由

m • AD =0 m • AS =0

，得

2c=0 2 a+ 2 b=0

，取b=-1，得a=1，c=0．
所以

m

=(1，-1，0)．
所以cos＜

m

，

n

＞=

m • n

| m |•| n |

=

- 2

3 • 2

=-

3

3

．
所以，平面SAD与平面SMC所成的二面角的正弦值为

6

3

．

点评：本题考查了平面与平面垂直的判定，考查了空间中的点线面见得距离的计算，考查了利用空间向量求解二面角的大小，综合考查了学生的空间想象能力和思维能力，是中档题．