题目内容
设x,y满足约束条件 ,w若目标函数z=ax+by(a>0,b>0)的值是最大值为12,则
,w若目标函数z=ax+by(a>0,b>0)的值是最大值为12,则 的最小值为( ).
的最小值为( ).
 ,w若目标函数z=ax+by(a>0,b>0)的值是最大值为12,则
,w若目标函数z=ax+by(a>0,b>0)的值是最大值为12,则 的最小值为( ).
的最小值为( ). A. | B. | C. | D.4 |
A
已知2a+3b=6,求  的最小值,可以作出不等式的平面区域,先用乘积进而用基本不等式解答.
的最小值,可以作出不等式的平面区域,先用乘积进而用基本不等式解答.
解答:解:不等式表示的平面区域如图所示阴影部分,

当直线ax+by=z(a>0,b>0)
过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,
目标函数z=ax+by(a>0,b>0)取得最大12,
即4a+6b=12,即2a+3b=6,而 =
=
≥ ,
,
故 的最小值为:
的最小值为: .
.
故答案选A
 的最小值,可以作出不等式的平面区域,先用乘积进而用基本不等式解答.
的最小值,可以作出不等式的平面区域,先用乘积进而用基本不等式解答.解答:解:不等式表示的平面区域如图所示阴影部分,

当直线ax+by=z(a>0,b>0)
过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,
目标函数z=ax+by(a>0,b>0)取得最大12,
即4a+6b=12,即2a+3b=6,而
 =
=
≥
 ,
,故
 的最小值为:
的最小值为: .
.故答案选A

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 满足条件
满足条件 则目标函数
则目标函数 的最大值为
的最大值为 满足
满足 ,使得
,使得 取最小值时的实数对
取最小值时的实数对 是
是



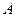 、
、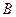 ,该所要根据该产品的研制成本、产品重量、搭载实验费用、和预计产生收益来决定具体安排.通过调查,有关数据如下表:
,该所要根据该产品的研制成本、产品重量、搭载实验费用、和预计产生收益来决定具体安排.通过调查,有关数据如下表: 满足条件
满足条件 则
则 的最小值是( )
的最小值是( ) 、
、 满足
满足 ,则
,则 的最大值为 .
的最大值为 . 下,目标函数
下,目标函数 的最大
的最大 值为____________
值为____________ 则
则
 取值范围是
取值范围是

