题目内容
已知函数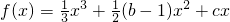 (b、c为常数),f(x)在x=1处和x=3处取得极值.
(b、c为常数),f(x)在x=1处和x=3处取得极值.
(Ι) 求f(x)的解析式;
(ΙΙ) 求f(x)的单调区间.
解:(Ι)∵函数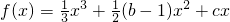 (b、c为常数),∴f′(x)=x2+(b-1)x+c.
(b、c为常数),∴f′(x)=x2+(b-1)x+c.
再由f(x)在x=1处和x=3处取得极值可得,1和3是方程 x2+(b-1)x+c=0的两个根.
∴1+3=b-1,1×3=c,解得 b=5,c=3.
故f(x)=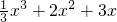 ,f′(x)=x2+4x+3.
,f′(x)=x2+4x+3.
(ΙΙ) 令f′(x)=x2+4x+3<0,解得-3<x<-1,故减区间为(-3,-1).
再 令f′(x)=x2+4x+3>0,解得 x>-1,或 x<-3,故增区间为(-∞,-3)、(-1,+∞).
分析:(Ι)先求出 f′(x)=x2+(b-1)x+c,再根据f(x)在x=1处和x=3处取得极值可得,1和3是方程 x2+(b-1)x+c=0的两个根,再利用根与系数的关系求出 b=5,c=3,
从而求出f(x)的解析式.
(ΙΙ) 令f′(x)=x2+4x+3<0,解得-3<x<-1,故减区间为(-3,-1).同理,令f′(x)>0,求出x的范围,即得增区间.
点评:本题主要考查利用导数研究函数的单调性,函数在某点取得极值的条件,求函数的解析式,属于中档题.
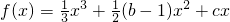 (b、c为常数),∴f′(x)=x2+(b-1)x+c.
(b、c为常数),∴f′(x)=x2+(b-1)x+c.再由f(x)在x=1处和x=3处取得极值可得,1和3是方程 x2+(b-1)x+c=0的两个根.
∴1+3=b-1,1×3=c,解得 b=5,c=3.
故f(x)=
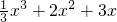 ,f′(x)=x2+4x+3.
,f′(x)=x2+4x+3.(ΙΙ) 令f′(x)=x2+4x+3<0,解得-3<x<-1,故减区间为(-3,-1).
再 令f′(x)=x2+4x+3>0,解得 x>-1,或 x<-3,故增区间为(-∞,-3)、(-1,+∞).
分析:(Ι)先求出 f′(x)=x2+(b-1)x+c,再根据f(x)在x=1处和x=3处取得极值可得,1和3是方程 x2+(b-1)x+c=0的两个根,再利用根与系数的关系求出 b=5,c=3,
从而求出f(x)的解析式.
(ΙΙ) 令f′(x)=x2+4x+3<0,解得-3<x<-1,故减区间为(-3,-1).同理,令f′(x)>0,求出x的范围,即得增区间.
点评:本题主要考查利用导数研究函数的单调性,函数在某点取得极值的条件,求函数的解析式,属于中档题.

练习册系列答案
相关题目
 ,则
,则