题目内容
在△ABC中角A，B，C所对的边分别为a，b，c，且c=b（2cosA+1）
（Ⅰ）若角B=30°，求角A；
（Ⅱ）若b（b+c）=16，求边a．
解：（Ⅰ）在△ABC中，由正弦定理得sinC=sinB（2cosA+1），
即sin（A+30°）=sin30°（2cosA+1）…2分
∴
sinA-
cosA=…4分
即sin（A-30°）=…6分
∵-30°＜A-30°＜150°，
∴A-30°=30°，得A=60°…8分
（Ⅱ）已知得cosA=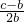
…9分
由余弦定理a2=b2+c2-2bccosA=b2+c2-2bc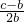=b2+bc=16…11分
得a=4…12分
分析：（Ⅰ）利用正弦定理将c=b（2cosA+1）化为sinC=sinB（2cosA+1），从而可求得sin（A-30°）=，可求得角A；
（Ⅱ）由c=b（2cosA+1）可求得cosA=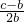，再结合余弦定理即可求得边a．
点评：本题考查正弦定理与余弦定理，考查三角函数间的关系，突出运算能力的考查，属于中档题．
即sin（A+30°）=sin30°（2cosA+1）…2分
∴
sinA-cosA=…4分即sin（A-30°）=
…6分∵-30°＜A-30°＜150°，
∴A-30°=30°，得A=60°…8分
（Ⅱ）已知得cosA=
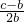…9分由余弦定理a2=b2+c2-2bccosA=b2+c2-2bc
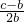=b2+bc=16…11分得a=4…12分
分析：（Ⅰ）利用正弦定理将c=b（2cosA+1）化为sinC=sinB（2cosA+1），从而可求得sin（A-30°）=
，可求得角A；（Ⅱ）由c=b（2cosA+1）可求得cosA=
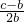，再结合余弦定理即可求得边a．点评：本题考查正弦定理与余弦定理，考查三角函数间的关系，突出运算能力的考查，属于中档题．
练习册系列答案
相关题目