题目内容
已知函数f(x)=cos .
.
(1)求函数f(x)的最小正周期及单调递增区间;
(2)若f(x)=1,求cos( )的值.
)的值.
解:(1)函数f(x)=cos =
=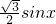 +
+ =sin(x+
=sin(x+ )+
)+ ,---(3分)
,---(3分)
所以函数f(x)的最小正周期为T=2π.-------(4分)
令 2kπ- ≤x+
≤x+ ≤2kπ+
≤2kπ+ ,k∈z,可得2kπ-
,k∈z,可得2kπ- ≤x+
≤x+ ≤2kπ+
≤2kπ+ ,k∈z.
,k∈z.
故函数y=f(x)的单调递增区间为[2kπ- ,2kπ+
,2kπ+ ],k∈z.-----------(6分)
],k∈z.-----------(6分)
(2)函数f(x)=sin(x+ )+
)+ =1,即 sin(x+
=1,即 sin(x+ )=
)= ,--------(7分)
,--------(7分)
故 cos( )=cos2(
)=cos2(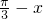 )═2cos2(
)═2cos2(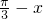 )-1=2
)-1=2 -1=-
-1=- . (12分)
. (12分)
分析:(1)利用两角和差的正弦公式、二倍角公式化简函数f(x)的解析式为sin(x+ )+
)+ ,由此可得函数的最小正周期,再令 2kπ-
,由此可得函数的最小正周期,再令 2kπ- ≤x+
≤x+ ≤2kπ+
≤2kπ+ ,k∈z,可得x的范围,即可求得单调递增区间.
,k∈z,可得x的范围,即可求得单调递增区间.
(2)由函数f(x)=1求得sin(x+ )=
)= ,再由cos(
,再由cos( )=cos2(
)=cos2(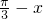 ) 利用二倍角公式、诱导公式求得结果.
) 利用二倍角公式、诱导公式求得结果.
点评:本题主要考查两角和差的正弦公式、二倍角公式、诱导公式的应用,正弦函数的周期性和单调性,属于中档题.
 =
=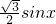 +
+ =sin(x+
=sin(x+ )+
)+ ,---(3分)
,---(3分)所以函数f(x)的最小正周期为T=2π.-------(4分)
令 2kπ-
 ≤x+
≤x+ ≤2kπ+
≤2kπ+ ,k∈z,可得2kπ-
,k∈z,可得2kπ- ≤x+
≤x+ ≤2kπ+
≤2kπ+ ,k∈z.
,k∈z.故函数y=f(x)的单调递增区间为[2kπ-
 ,2kπ+
,2kπ+ ],k∈z.-----------(6分)
],k∈z.-----------(6分)(2)函数f(x)=sin(x+
 )+
)+ =1,即 sin(x+
=1,即 sin(x+ )=
)= ,--------(7分)
,--------(7分)故 cos(
 )=cos2(
)=cos2(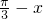 )═2cos2(
)═2cos2(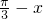 )-1=2
)-1=2 -1=-
-1=- . (12分)
. (12分)分析:(1)利用两角和差的正弦公式、二倍角公式化简函数f(x)的解析式为sin(x+
 )+
)+ ,由此可得函数的最小正周期,再令 2kπ-
,由此可得函数的最小正周期,再令 2kπ- ≤x+
≤x+ ≤2kπ+
≤2kπ+ ,k∈z,可得x的范围,即可求得单调递增区间.
,k∈z,可得x的范围,即可求得单调递增区间.(2)由函数f(x)=1求得sin(x+
 )=
)= ,再由cos(
,再由cos( )=cos2(
)=cos2(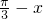 ) 利用二倍角公式、诱导公式求得结果.
) 利用二倍角公式、诱导公式求得结果.点评:本题主要考查两角和差的正弦公式、二倍角公式、诱导公式的应用,正弦函数的周期性和单调性,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,则关于x的方程f2(x)+bf(x)+c=0有5个不同实数解的充要条件是( )
|
| A、b<-2且c>0 |
| B、b>-2且c<0 |
| C、b<-2且c=0 |
| D、b≥-2且c=0 |
 已知函数f(x)的图象如图所示,则函数的值域为( )
已知函数f(x)的图象如图所示,则函数的值域为( )