题目内容
下表给出了从某校500名12岁的男生中用简单随机抽样得出的120人的身高资料(单位:厘米).区间界限 | ［122，126 | ［126，130 | ［130，134 | ［134，138 | ［138，142 |
人数 | 5 | 8 | 10 | 22 | 33 |
区间界限 | ［142，166 | ［146，150 | ［150，154 | ［154，158 |
|
人数 | 20 | 11 | 6 | 5 |
|
（1）列出样本的频率分布表；
（2）画出频率分布直方图；
（3）估计身高低于134厘米的人数占总人数的百分比和身高在区间［134，146）（厘米）内的人数占总人数的百分比.
解:(1)样本频率分布表:
分组 | 频数 | 频率 |
［122,126) | 5 | 0.04 |
［126,130) | 8 | 0.07 |
［130,134) | 10 | 0.08 |
［134,138) | 22 | 0.18 |
［138,142) | 33 | 0.28 |
［142,146) | 20 | 0.17 |
［146,150) | 11 | 0.09 |
［150,154) | 6 | 0.05 |
［154,158) | 5 | 0.04 |
合 计 | 120 | 1.00 |
(2)样本的频率分布直方图:
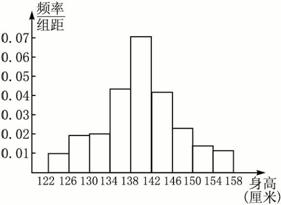
(3)∵样本中身高低于134厘米的男生出现的频率为
=0.19,
∴由样本频率可估计该校身高低于134厘米的男生占这500名12岁男生总数的19%.
∵样本中身高在区间［134,146)(厘米)内的男生出现的频率为
=0.625，
∴估计该校500名12岁男生中身高在区间［134,146］(厘米)内的有62.5%.
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案（本题满分12分）
某校为了探索一种新的教学模式，进行了一项课题实验，乙班为实验班，甲班为对比班，甲乙两班的人数均为50人，一年后对两班进行测试，成绩如下表（总分：150分）：
甲班
|
成绩 |
|
|
|
|
|
|
频数 |
4 |
20 |
15 |
10 |
1 |
乙班
|
成绩 |
|
|
|
|
|
|
频数 |
1 |
11 |
23 |
13 |
2 |
（1）现从甲班成绩位于
内的试卷中抽取9份进行试卷分析，请问用什么抽样方法更合理，并写出最后的抽样结果；
（2）根据所给数据可估计在这次测试中，甲班的平均分是101.8，请你估计乙班的平均分，并计算两班平均分相差几分；
（3）完成下面2×2列联表，你认为在犯错误的概率不超过0.025的前提下， “这两个班在这次测试中成绩的差异与实施课题实验有关”吗？并说明理由。
|
|
成绩小于100分 |
成绩不小于100分 |
合计 |
|
甲班 |
|
26 |
50 |
|
乙班 |
12 |
|
50 |
|
合计 |
36 |
64 |
100 |
附：
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
18.
下表给出了从某校500名12岁男生中用简单随机抽样得出的120人的身高资料（单位：厘米）：
（1）在这个问题中，总体是什么？
| 分组 | 人数 | 频率 |
| [122，126 ） | 5 | 0.042 |
| [126，130） | 8 | 0.067 |
| [130，134 ） | 10 | 0.083 |
| [134，138） | 22 | 0.183 |
| [138，142） | y | |
| [142，146） | 20 | 0.167 |
| [146，150） | 11 | 0.092 |
| [150，154） | x | 0.050 |
| [154，158） | 5 | 0.042 |
| 合计 | 120 | 1.00 |
（3）试计算身高在134﹏146cm的总人数约有多少？
