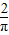题目内容
若点（a，b）是圆x2+（y+1）2=1内的动点，则函数f（x）=x2+ax+b的一个零点在（-1，0）内，另一个零点在（0，1）内的概率为
- A.
- B.
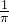
- C.
- D.
A
分析：根据几何概型的意义，关键是要找出数f（x）=x2+ax+b的一个零点在（-1，0）内，另一个零点在（0，1）内对应的可行域的大小，及a，b取值范围对应区域的大小，再根据几何概型计算公式求解．
解答：
解：由已知得：
其表示得区域M如图阴影部分，它在圆x2+（y+1）2=1内的部分的面积是圆的面积的．
∴P=
故选A．
点评：几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P=N（A）/N求解．
分析：根据几何概型的意义，关键是要找出数f（x）=x2+ax+b的一个零点在（-1，0）内，另一个零点在（0，1）内对应的可行域的大小，及a，b取值范围对应区域的大小，再根据几何概型计算公式求解．
解答：
解：由已知得：其表示得区域M如图阴影部分，它在圆x2+（y+1）2=1内的部分的面积是圆的面积的
．∴P=
故选A．
点评：几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P=N（A）/N求解．
练习册系列答案
相关题目
若函数f ( x )=-
lnx的图象在x=1处的切线l过点( 0 ， -
)，且l与圆C：x2+y2=1相交，则点（a，b）与圆C的位置关系是（ ）
| a |
| b |
| 1 |
| b |
| A、点在圆内 | B、点在圆外 |
| C、点在圆上 | D、不能确定 |
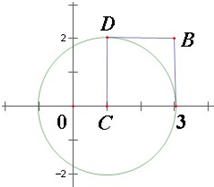已知圆C：（x-1）2+y2=4，点（a，b）．
