题目内容
16.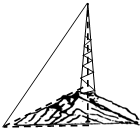 如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30米,在地面上
如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30米,在地面上有一点A,测得A,C间的距离为78米,从A观测电视发射塔CD的视角(∠CAD)为
45°,则这座电视发射塔的高度CD约为145.米(结果保留到整数).
分析 根据勾股定理求得AB,进而求得tan∠CAB,再通过tan∠DAB=tan(∠DAC+∠CAB)利用正切两角和公式,求得DC.
解答 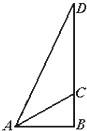 解:如图,$AB=\sqrt{{{78}^2}-{{30}^2}}=72$,$tan∠CAB=\frac{CB}{AB}=\frac{30}{72}=\frac{5}{12}$.
解:如图,$AB=\sqrt{{{78}^2}-{{30}^2}}=72$,$tan∠CAB=\frac{CB}{AB}=\frac{30}{72}=\frac{5}{12}$.
由$\frac{DC+30}{72}=tan({45°}+∠CAB)=\frac{{1+\frac{5}{12}}}{{1-\frac{5}{12}}}=\frac{17}{7}$,得7CD=1014⇒CD≈145.
故答案为:145.
点评 本题主要考查了三角形的实际应用,属基础题.

练习册系列答案
相关题目
4.若函数f(x)=$\frac{ax+1}{x+2}$在(-2,2)内为增函数,则实数a的取值范围是( )
| A. | ($\frac{1}{2}$,+∞) | B. | [$\frac{1}{2}$,+∞) | C. | (-∞,$\frac{1}{2}$) | D. | (-∞,$\frac{1}{2}$] |
1.因为对数函数y=logax(a>0,且a≠1)是增函数,而y=log${\;}_{\frac{1}{2}}$x是对数函数,所以y=log${\;}_{\frac{1}{2}}$x是增函数,上面的推理错误的是( )
| A. | 大前提 | B. | 小前提 | C. | 推理形式 | D. | 以上都是 |
5.如图给出的是计算和式$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个程序框图,其中判断框内应填入的条件是( )
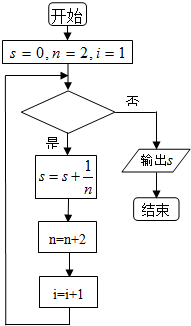

| A. | i≤11 | B. | i≤10 | C. | i≥10 | D. | i≥11 |
6.已知f(x)=$\left\{\begin{array}{l}{3|lo{g}_{3}x|,0<x≤3}\\{(x-4)(x-6),x>3}\end{array}\right.$,若f(a)=f(b)=f(c)=f(d),且a<b<c<d,则abcd的取值范围是( )
| A. | (23,24) | B. | (24,27) | C. | (21,24) | D. | (24,25) |