题目内容
在直角坐标系 上取两个定点
上取两个定点 ,再取两个动点
,再取两个动点
 ,且
,且 .
.
(Ⅰ)求直线 与
与 交点的轨迹
交点的轨迹 的方程;
的方程;
(Ⅱ)已知点 (
( )是轨迹
)是轨迹 上的定点,
上的定点, 是轨迹
是轨迹 上的两个动点,如果直线
上的两个动点,如果直线 的斜率
的斜率 与直线
与直线 的斜率
的斜率 满足
满足 ,试探究直线
,试探究直线 的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
【答案】
解:(Ⅰ)轨迹M的方程为 (
( )
)
(Ⅱ)直线EF的斜率为定值,其值为
【解析】本试题主要考查了直线与直线的位置关系,以及直线与椭圆的位置关系的综合运用。(1) 依题意知直线 的方程为:
的方程为: ,直线
,直线 的方程为:
的方程为: ,利用交轨法得到轨迹方程的求解。
,利用交轨法得到轨迹方程的求解。
(2)设出直线方程与椭圆方程联立,运用韦达定理,和斜率公示得到结论。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 上取两个定点
上取两个定点 ,再取两个动点
,再取两个动点 且
且 .
. 与
与 交点的轨迹
交点的轨迹 的方程;
的方程; ,设直线:
,设直线: 与(I)中的轨迹
与(I)中的轨迹 、
、 两点,直线
两点,直线 、
、 的倾斜角分别为
的倾斜角分别为 且
且 ,求证:直线过定点,并求该定点的坐标.
,求证:直线过定点,并求该定点的坐标. 上取两个定点
上取两个定点 ,再取两个动点
,再取两个动点 
 ,且
,且 .
. 与
与 交点的轨迹
交点的轨迹 的方程;
的方程; (
( )是轨迹
)是轨迹 是轨迹
是轨迹 的斜率
的斜率 与直线
与直线 的斜率
的斜率 满足
满足 ,试探究直线
,试探究直线 的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.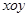 上取两个定点
上取两个定点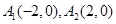 ,再取两个动点
,再取两个动点
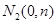 ,且
,且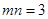
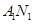 与
与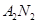 交点的轨迹
交点的轨迹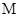 的方程
的方程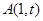 (
(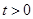 )是轨迹
)是轨迹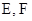 是轨迹
是轨迹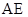
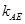 与直线
与直线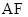 的斜率
的斜率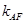 满足
满足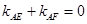 ,试探究直线
,试探究直线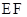 的斜率是否是
的斜率是否是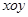 上取两个定点
上取两个定点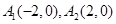 ,再取两个动点
,再取两个动点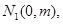
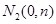 ,且
,且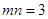
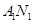 与
与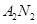 交点的轨迹
交点的轨迹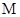 的方程
的方程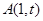 (
(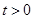 )是轨迹
)是轨迹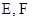 是轨迹
是轨迹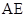
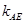 与直线
与直线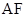 的斜率
的斜率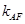 满足
满足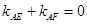 ,试探究直线
,试探究直线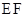 的斜率是否是
的斜率是否是