题目内容
2．抛物线y=-2x2的焦点坐标为（ ）| A． | （-$\frac{1}{8}$，0） | B． | （$\frac{1}{4}$，0） | C． | （0，-$\frac{1}{8}$） | D． | （0，-$\frac{1}{4}$） |
分析 化抛物线方程为标准方程，确定其焦点位置，再求抛物线的焦点坐标．
解答 解：抛物线y=-2x2，化为标准方程为：x2=-$\frac{1}{2}$y
∴抛物线的焦点在y轴的负半轴上，且2p=$\frac{1}{2}$
∴$\frac{p}{2}$=$\frac{1}{8}$，
∴抛物线y=-2x2的焦点坐标为（0，-$\frac{1}{8}$）
故选：C．
点评 本题考查抛物线的几何性质，化抛物线方程为标准方程是解题的关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13．定义在（0，+∞）的函数f（x）非负实数，且满足xf′（x）＜f（x），若m，n∈（0，+∞）且m＜n，则必有（ ）
| A． | nf（n）＜mf（m） | B． | nf（m）＜mf（n） | C． | mf（m）＜nf（n） | D． | mf（n）＜nf（m） |
14．已知函数y=f（x）是定义在R上的奇函数，当x≥0时，$f（x）=\root{3}{x}（1+x）$，则当x＜0时，f（x）的表达式是（ ）
| A． | $f（x）=\root{3}{x}（1-x）$ | B． | $f（x）=-\root{3}{x}（1-x）$ | C． | $f（x）=\root{3}{x}（1+x）$ | D． | $f（x）=-\root{3}{x}（1+x）$ |
11．
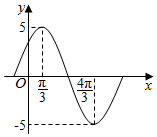已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象如图所示，若f（α）=3，α∈（$\frac{π}{3}$，$\frac{5π}{6}$），则sinα的值为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象如图所示，若f（α）=3，α∈（$\frac{π}{3}$，$\frac{5π}{6}$），则sinα的值为（ ）| A． | $\frac{3\sqrt{3}+4}{10}$ | B． | $\frac{3\sqrt{3}-4}{10}$ | C． | $\frac{3+4\sqrt{3}}{10}$ | D． | $\frac{3-4\sqrt{3}}{10}$ |