题目内容
 已知三棱柱A1B1C1-ABC中,三个侧面均为矩形,底面ABC为等腰直角三角形,C1C=CA=CB=2,点D为棱CC1的中点,点E在棱B1C1上运动.
已知三棱柱A1B1C1-ABC中,三个侧面均为矩形,底面ABC为等腰直角三角形,C1C=CA=CB=2,点D为棱CC1的中点,点E在棱B1C1上运动.(I)求证A1C⊥AE;
(II)当点E到达某一位置时,恰使二面角E-A1D-B的平面角的余弦值为
| ||
| 6 |
| C1E |
| C1B1 |
(III)在(II)的条件下,在平面ABC上确定点F,使得EF⊥平面A1DB?并求出EF的长度.
分析:(I)以CB为x轴,CA为y轴,CC1为z轴,C为原点建立坐标系,设E(m,0,2),要证A1C⊥AE,可证
⊥
,只需证明
=0,利用向量的数量积运算即可证明;
(II)分别求出平面EA1D、平面A1DB的一个法向量,由两法向量夹角余弦值的绝对值等于
,解得m值,由此可得答案;
(III)在(II)的条件下,设F(x,y,0),可知
与平面A1DB的一个法向量平行,由此可求出点F坐标,进而求出|
|,即得答案;
| A1C |
| AE |
| A1C |
| • |
| AE |
(II)分别求出平面EA1D、平面A1DB的一个法向量,由两法向量夹角余弦值的绝对值等于
| ||
| 6 |
(III)在(II)的条件下,设F(x,y,0),可知
| EF |
| EF |
解答:解:(I)以CB为x轴,CA为y轴,CC1为z轴,C为原点建立坐标系,设E(m,0,2),
C(0,0,0),A(0,2,0),A1(0,2,2),D(0,0,1),B(2,0,0),
=(0,-2,-2),
=(m,-2,2),
因为
=0+(-2)×(-2)-2×2=0,
所以
⊥
,即A1C⊥AE;
(II)
=(m,0,1),
=(0,2,1),
设
=(x,y,z)为平面EA1D的一个法向量,
则
,即
,取
=(2,m,-2m),
=(2,0,-1),设
=(x,y,z)为平面A1DB的一个法向量,
则
,即
,取
=(1,-1,2),
由二面角E-A1D-B的平面角的余弦值为
,得|
|=
,解得m=1,
所以
=
;
(III)由(II)知E(1,0,2),且
=(1,-1,2)为平面A1DB的一个法向量,
设F(x,y,0),则
=(x-1,y,-2),且
∥
,所以x-1=-1,y=1,解得x=0,y=1,
所以
=(-1,1,-2),|
|=
=
,
故EF的长度为
,此时点F(0,1,0).
C(0,0,0),A(0,2,0),A1(0,2,2),D(0,0,1),B(2,0,0),
| A1C |
| AE |
因为
| A1C |
| • |
| AE |
所以
| A1C |
| AE |
(II)
| DE |
| DA1 |
设
| n |
则
|
|
| n |
| DB |
| n |
则
|
|
| n |
由二面角E-A1D-B的平面角的余弦值为
| ||
| 6 |
| 2-m-4m | ||||
|
| ||
| 6 |
所以
| C1E |
| C1B1 |
| 1 |
| 2 |
(III)由(II)知E(1,0,2),且
| n |
设F(x,y,0),则
| EF |
| EF |
| n |
所以
| EF |
| EF |
| (-1)2+12+(-2)2 |
| 6 |
故EF的长度为
| 6 |
点评:本题考查重点考查直线与平面垂直的性质、二面角的平面角及其求法、空间点、线、面间距离计算,考查学生空间想象能力、推理论证能力.

练习册系列答案
相关题目
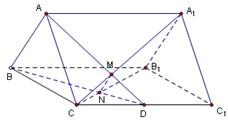 如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,平面ABD和平面A1B1C的交线为MN.
如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,平面ABD和平面A1B1C的交线为MN.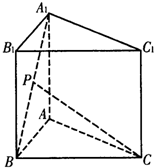 已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B上的点,且PC⊥AB
已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B上的点,且PC⊥AB 如图,在三棱柱ABC-A1B1C中,已知AC⊥BC,AB⊥BB1,CD⊥平面AA B1B,AC=BC=2.
如图,在三棱柱ABC-A1B1C中,已知AC⊥BC,AB⊥BB1,CD⊥平面AA B1B,AC=BC=2. (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=