题目内容
已知集合A={1},B={2,3},C={3,4,5},从这三个集合中各取一个元素构成空间直角坐标系中的点的坐标,则确定的不同点的个数是( )
| A.33 | B.34 | C.35 | D.36 |
不考虑限定条件确定的不同点的个数为C21C31A33=36,
但集合B、C中有相同元素1,
由1,3,3三个数确定的不同点的个数只有三个,不是
=6个,
故所求的不同点的个数为36-3=33个,
故选A.
但集合B、C中有相同元素1,
由1,3,3三个数确定的不同点的个数只有三个,不是
| A | 33 |
故所求的不同点的个数为36-3=33个,
故选A.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
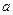 个,四位偶数有
个,四位偶数有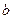 个,求
个,求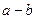 的值;
的值;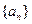 ,求
,求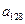 .
.