题目内容
如图,在几何体SABCD中,AD⊥平面SCD,BC⊥平面SCD,AD=DC=2,BC=1,又SD=2,,∠SDC=120°.(1)求SC与平面SAB所成角的正弦值;
(2)求平面SAD与平面SAB所成的锐二面角的余弦值.
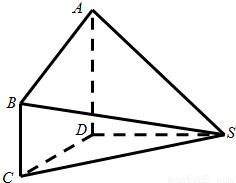
【答案】分析:如图,过点D作DC的垂线交SC于E,以D为原点,分别以DC,DE,DA为x,y,z轴建立空间上角坐标系,
(1)设平面SAB的法向量为 ,利用
,利用 ,得
,得 ,设SC与平面SAB所成角为θ,
,设SC与平面SAB所成角为θ,
通过 ,求出SC与平面SAB所成角的正弦值为
,求出SC与平面SAB所成角的正弦值为 .
.
(2)设平面SAD的法向量为 ,利用
,利用 ,得
,得 .利用
.利用 ,求出平面SAD与平面SAB所成的锐二面角的余弦值是
,求出平面SAD与平面SAB所成的锐二面角的余弦值是 .
.
解答: 解:如图,过点D作DC的垂线交SC于E,以D为原点,
解:如图,过点D作DC的垂线交SC于E,以D为原点,
分别以DC,DE,DA为x,y,z轴建立空间上角坐标系.
∵∠SDC=120°,
∴∠SDE=30°,
又SD=2,则点S到y轴的距离为1,到x轴的距离为 .
.
则有D(0,0,0), ,A(0,0,2),C(2,0,0),B(2,0,1).(4分)
,A(0,0,2),C(2,0,0),B(2,0,1).(4分)
(1)设平面SAB的法向量为 ,
,
∵ .
.
则有 ,取
,取 ,
,
得 ,又
,又 ,
,
设SC与平面SAB所成角为θ,
则 ,
,
故SC与平面SAB所成角的正弦值为 .(9分)
.(9分)
(2)设平面SAD的法向量为 ,
,
∵ ,
,
则有 ,取
,取 ,得
,得 .
.
∴ ,
,
故平面SAD与平面SAB所成的锐二面角的余弦值是 .(14分)
.(14分)
点评:本题是中档题,考查直线与平面所成角正弦值、余弦值的求法,考查空间想象能力,计算能力,熟练掌握基本定理、基本方法是解决本题的关键.
(1)设平面SAB的法向量为
 ,利用
,利用 ,得
,得 ,设SC与平面SAB所成角为θ,
,设SC与平面SAB所成角为θ,通过
 ,求出SC与平面SAB所成角的正弦值为
,求出SC与平面SAB所成角的正弦值为 .
.(2)设平面SAD的法向量为
 ,利用
,利用 ,得
,得 .利用
.利用 ,求出平面SAD与平面SAB所成的锐二面角的余弦值是
,求出平面SAD与平面SAB所成的锐二面角的余弦值是 .
.解答:
 解:如图,过点D作DC的垂线交SC于E,以D为原点,
解:如图,过点D作DC的垂线交SC于E,以D为原点,分别以DC,DE,DA为x,y,z轴建立空间上角坐标系.
∵∠SDC=120°,
∴∠SDE=30°,
又SD=2,则点S到y轴的距离为1,到x轴的距离为
 .
.则有D(0,0,0),
 ,A(0,0,2),C(2,0,0),B(2,0,1).(4分)
,A(0,0,2),C(2,0,0),B(2,0,1).(4分)(1)设平面SAB的法向量为
 ,
,∵
 .
.则有
 ,取
,取 ,
,得
 ,又
,又 ,
,设SC与平面SAB所成角为θ,
则
 ,
,故SC与平面SAB所成角的正弦值为
 .(9分)
.(9分)(2)设平面SAD的法向量为
 ,
,∵
 ,
,则有
 ,取
,取 ,得
,得 .
.∴
 ,
,故平面SAD与平面SAB所成的锐二面角的余弦值是
 .(14分)
.(14分)点评:本题是中档题,考查直线与平面所成角正弦值、余弦值的求法,考查空间想象能力,计算能力,熟练掌握基本定理、基本方法是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在几何体SABCD中,AD⊥平面SCD,BC⊥平面SCD,AD=DC=2,BC=1,又SD=2,,∠SDC=120°.
如图,在几何体SABCD中,AD⊥平面SCD,BC⊥平面SCD,AD=DC=2,BC=1,又SD=2,,∠SDC=120°.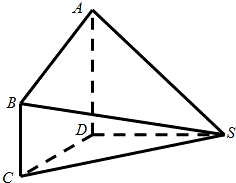 如图,在几何体SABCD中,AD⊥平面SCD,BC⊥平面SCD,AD=DC=2,BC=1,又SD=2,,∠SDC=120°.
如图,在几何体SABCD中,AD⊥平面SCD,BC⊥平面SCD,AD=DC=2,BC=1,又SD=2,,∠SDC=120°.