题目内容
已知函数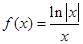
(I)求函数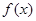 的单调区间; (II)若关于
的单调区间; (II)若关于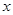 的不等式
的不等式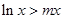 对一切
对一切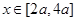 都成立
都成立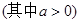 ,求实数
,求实数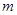 的取值范围.
的取值范围.
【答案】
(I) 的单调增区间为
的单调增区间为 和
和 ;单调减区间为
;单调减区间为 和
和 .
.
(II)当 时,
时,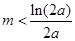 ;当
;当 时,
时, .
.
【解析】求函数 的单调区间时,一定注意函数的定义域,尤其对于对数函数;
的单调区间时,一定注意函数的定义域,尤其对于对数函数;
对于恒成立求参数问题,通常分离参数,然后只要求在最值处成立即可,关于 的不等式
的不等式 对一切
对一切 都成立
都成立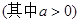

 ,然后分析函数的最值时利用导数求出单调区间。
,然后分析函数的最值时利用导数求出单调区间。
解:(I) ,当
,当 时,
时,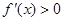 ;当
;当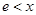 时,
时, ,
,
所以 在
在 上单调递增,在
上单调递增,在 上单调递减.又函数
上单调递减.又函数 为奇函数,所以
为奇函数,所以 在
在 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
∴ 的单调增区间为
的单调增区间为 和
和 ;单调减区间为
;单调减区间为 和
和 .
.
(II)不等式 对一切
对一切 都成立,即
都成立,即 对一切
对一切 都成立
都成立
由(I)知 在
在 上单调递增,在
上单调递增,在 上单调递减,所以,
上单调递减,所以,
当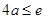 ,即
,即 时,
时, 在
在 上单调递增,
上单调递增, ;
;
当 ,即
,即 时,
时, 在
在 上单调递减,
上单调递减,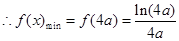 ;
;
当 ,即
,即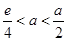 时,
时, 在
在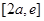 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
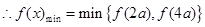 .下面比较
.下面比较 的大小:
的大小:
 ,∴当
,∴当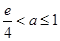 时,
时, ,当
,当 时,
时,
综上得:当 时,
时, ;当
;当 时,
时, .
.
故当 时,
时,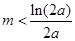 ;当
;当 时,
时, .
.

练习册系列答案
相关题目
 的 部 分 图 象如 图 所示.
的 部 分 图 象如 图 所示. 的
解 析 式;
的
解 析 式; 中,角
中,角 的
对 边 分 别 是
的
对 边 分 别 是 ,若
,若 的
取 值 范 围.
的
取 值 范 围.