题目内容
已知直线l1为曲线y=x2+x-2在点(1,0)处的切线,l2为该曲线的另一条切线,且l1⊥l2.(1)求直线l2的方程;
(2)求由直线l1、l2和x轴所围成的三角形的面积.
思路分析:本题考查直线方程和三角形面积.
(1)求曲线在某点处的切线方程步骤:先求曲线在这点处的导数,这点对应的导数值即为过此点切线的斜率.再用点斜式写出直线方程.(2)求面积用S=![]() a·h即可完成.
a·h即可完成.
解:(1)y′=2x+1,直线l1的方程为y=3x-3,
设直线l2过曲线y=x2+x-2上的点B(b,b2+b-2),
则l2的方程为y=(2b+1)x-b2-2.
因为l1⊥l2,则有2b+1=-![]() ,b=-
,b=-![]() .
.
所以直线l2的方程为y=-![]() x-
x-![]() .
.
(2)解方程组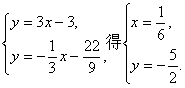
所以直线l1和l2的交点坐标为(![]() ).
).
l1、l2与x轴交点的坐标分别为(1,0)、(-![]() ,0),
,0),
故所求三角形的面积S=![]() ×
×![]() ×|-
×|-![]() |=
|=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目