题目内容
已知圆C以![]() 为圆心,5为半径,过点S
为圆心,5为半径,过点S![]() 作直线
作直线![]() 与圆C交于A,B两点.
与圆C交于A,B两点.
(1)若AB=8,求直线![]() 的方程;
的方程;
(2)当直线![]() 的斜率为
的斜率为![]() 时,在
时,在![]() 上求一点P,使P到圆C的切线长等于PS;
上求一点P,使P到圆C的切线长等于PS;
(3)设AB的中点为N,试在平面上找一定点M,使MN的长为定值
(1)![]() 或
或![]()
(2)点![]() 的坐标为
的坐标为![]()
(3)定点M的坐标为![]()
解析:
(1)圆的方程是![]() ……………1分
……………1分
由条件可知:圆心C到直线![]() 的距离为3.……………………3分
的距离为3.……………………3分
当斜率不存在时,![]() 符合条件;…………………………4分
符合条件;…………………………4分
当斜率存在时,根据点到直线的距离公式求得![]() 的方程为
的方程为![]() .
.
∴直线![]() 方程是
方程是![]() 或
或![]() .………………6分
.………………6分
(2)当![]() 斜率为-2时,直线
斜率为-2时,直线![]() 方程为
方程为![]() ,
,
根据题意,有![]() ……10分
……10分
解之得 ![]() .
.
∴点![]() 的坐标为
的坐标为![]() .……………12分
.……………12分
(3)定点M的坐标为![]() ,由直角三角形斜边上的中线等于斜边一半可得…16分
,由直角三角形斜边上的中线等于斜边一半可得…16分

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 如图,
如图, 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于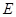 .
. 的长.
的长. ,其中
,其中 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
. 的极坐标方程为
的极坐标方程为 ,
,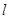 与圆相交于
与圆相交于 ,A两点,且∠
,A两点,且∠ ,求
,求 的长.
的长. ,且与圆相切的直线的极坐标方程;
,且与圆相切的直线的极坐标方程; 满足
满足 ,求
,求 的最小值;
的最小值; 如图,
如图, 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以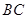 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于 .
. 的长.
的长. ,其中
,其中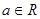 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
. 的极坐标方程为
的极坐标方程为 ,
, 与圆相交于
与圆相交于 ,A两点,且∠
,A两点,且∠ ,求
,求 的长.
的长. ,且与圆相切的直线的极坐标方程;
,且与圆相切的直线的极坐标方程; 满足
满足 ,求
,求 的最小值;
的最小值;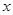 轴上,左右焦点分别为
轴上,左右焦点分别为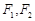 ,且
,且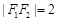 ,点(1,
,点(1,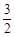 )在椭圆C上.
)在椭圆C上.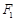 的直线
的直线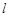 与椭圆
与椭圆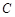 相交于
相交于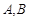 两点,且
两点,且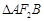 的面积为
的面积为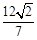 ,求以
,求以 为圆心且与直线
为圆心且与直线