题目内容
如图,在直三棱柱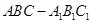 中,
中,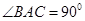 ,
,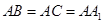 .
.
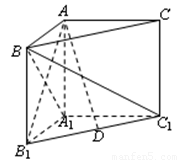
(Ⅰ)求证: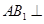 平面
平面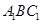 ;
;
(Ⅱ)若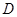 为
为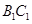 的中点,求
的中点,求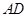 与平面
与平面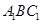 所成的角.
所成的角.
【答案】
(1)证明过程详见解析;(2)所成的角为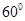 .
.
【解析】
试题分析:本题主要考查空间线、面位置关系,线面所成的角等基础知识,同时考查空间想象能力和推理论证能力.第一问,先利用正方形得对角线互相垂直 ,再利用线面垂直得到线线垂直
,再利用线面垂直得到线线垂直 ,再利用线面垂直的判定定理得到线面垂直
,再利用线面垂直的判定定理得到线面垂直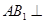 平面
平面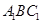 ;第二问,先由已知条件判断
;第二问,先由已知条件判断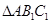 是正三角形,由第一问的结论可知,
是正三角形,由第一问的结论可知,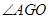 是
是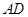 与平面
与平面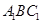 所成的角,在直角
所成的角,在直角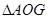 中,得出
中,得出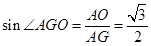 ,所以
,所以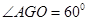 ,即
,即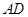 与平面
与平面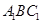 所成的角为
所成的角为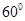 .
.
试题解析:(Ⅰ) 由题意知四边形 是正方形,故
是正方形,故 .
.
由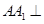 平面
平面 ,得
,得 .
.
又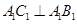 ,所以
,所以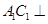 平面
平面 ,故
,故 .
.
从而得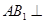 平面
平面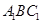 . 7分
. 7分
(Ⅱ)设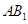 与
与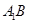 相交于点
相交于点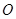 ,则点
,则点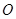 是线段
是线段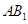 的中点.
的中点.
连接 ,由题意知
,由题意知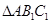 是正三角形.
是正三角形.
由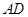 ,
,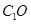 是
是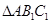 的中线知:
的中线知: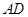 与
与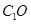 的交点为重心
的交点为重心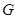 ,连接
,连接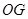 .
.
由(Ⅰ)知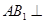 平面
平面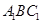 ,故
,故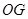 是
是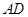 在平面
在平面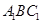 上的射影,于是
上的射影,于是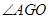 是
是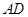 与平面
与平面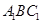 所成的角.
所成的角.
在直角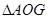 中,
中,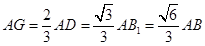 ,
, 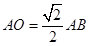 ,
,
所以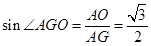 .
.
故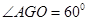 ,即
,即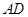 与平面
与平面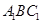 所成的角为
所成的角为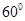 . 15分
. 15分
考点:1.线面垂直的判定定理;2.线面垂直的性质;3.中线的性质;4.直角三角形中求正弦.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
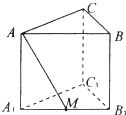 如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1=
如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1= 中, AB=1,
中, AB=1, ,
, .
. ;
; —B的正切值。
—B的正切值。
 中,
中, ,
, 分别为
分别为 的中点,四边形
的中点,四边形 是边长为
是边长为 的正方形.
的正方形. 平面
平面 ;
; 平面
平面 的余弦值.
的余弦值.
 中,
中, ,
, ,
, 是
是 的中点.
的中点. ∥平面
∥平面 ;
; 的余弦值;
的余弦值; 上是否存在点
上是否存在点 ,使
,使 与
与 成
成 角?若存在,确定
角?若存在,确定
 中,
中, ,点
,点 是
是 的中点.
的中点. ;(2)
;(2) 平面
平面 .
.