题目内容
1.以曲线C:y=x2(x≥0)上某一点A为切点作一切线l,使之与曲线C以及x轴所围成的图形的面积为$\frac{2}{3}$,求切线l的方程.分析 求切点A的坐标及过切点A的切线方程,先求切点A的坐标,设点A的坐标,只须在切点处的切线方程,故先利用导数求出在切点处的导函数值,再结合导数的几何意义即可求出切线的斜率从而得到切线的方程进而求得面积的表达式.最后建立方程解之即得.最后求出其斜率的值即可,即导数值即可求出切线的斜率.从而问题解决.
解答 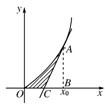 解:如图所示,设切点A(x0,y0),
解:如图所示,设切点A(x0,y0),
由y′=2x,得过点A的切线方程为
y-y0=2x0(x-x0),即y=2x0x-x02.
令y=0,得x=$\frac{{x}_{0}}{2}$,即C($\frac{{x}_{0}}{2}$,0).
设由曲线和过A点的切线及x轴所围成图形的面积为S.
S曲边三角形AOB=${∫}_{0}^{{x}_{0}}$x2dx=$\frac{1}{3}$x3|${\;}_{0}^{{x}_{0}}$=$\frac{1}{3}$x03,
S△ABC=$\frac{1}{2}$|BC|•|AB|=$\frac{1}{2}$(x0-$\frac{{x}_{0}}{2}$)•x02=$\frac{1}{4}$x03.
∴S=$\frac{1}{3}$x03-$\frac{1}{4}$x03=$\frac{1}{12}$x03=$\frac{2}{3}$.
∴x0=2,即有切线方程为y=4x-4.
点评 本题主要考查利用导数研究曲线上某点切线方程、定积分的应用、直线的方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
相关题目
12.设等差数列{an}的前n项和为Sn,且满足S20>0,S21<0,则$\frac{S_1}{a_1},\frac{S_2}{a_2},…,\frac{{{S_{21}}}}{{{a_{21}}}}$中最大的项为( )
| A. | $\frac{s_8}{a_8}$ | B. | $\frac{{{s_{10}}}}{{{a_{10}}}}$ | C. | $\frac{{{s_{11}}}}{{{a_{11}}}}$ | D. | $\frac{{S}_{9}}{{a}_{9}}$ |
16. 某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的直角三角形,该几何体体积是( )
某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的直角三角形,该几何体体积是( )
 某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的直角三角形,该几何体体积是( )
某几何体的三视图如图所示,其中正视图是两底边长分别为1,2的直角梯形,俯视图是斜边长为3的直角三角形,该几何体体积是( )| A. | 1 | B. | 2 | C. | $\frac{7}{4}$ | D. | $\frac{9}{4}$ |
6.已知a>0,b>0,双曲线S:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1的离心率为3,k是双曲线S的一条渐近线的斜率,如果k>0,那么$\frac{k}{a}$+b的最小值为( )
| A. | 2 | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 6 |
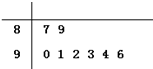 某校高二年级8个班参加合唱比赛的得分如面茎叶图所示,则这组数据的中位数和平均数为91.5和91.5.
某校高二年级8个班参加合唱比赛的得分如面茎叶图所示,则这组数据的中位数和平均数为91.5和91.5.