题目内容
已知函数g(x)=| 1 |
| 2 |
| 2 |
| x |
(Ⅰ)判断函数g(x)的奇偶性;
(Ⅱ)求函数g(x)在区间[1,4]上的最大值和最小值.
分析:(I)求出定义域;求出g(-x),判断g(-x),g(x)的关系;利用奇函数的定义判断出g(x)为奇函数.
(II)求出g(x)的导函数,求出导函数的根,判断根左右两边的导函数符号,求出函数的最值.
(II)求出g(x)的导函数,求出导函数的根,判断根左右两边的导函数符号,求出函数的最值.
解答:解:(I)函数的定义域为x≠0
g(-x)=
(-x-
)=-
(x+
)=-g(x)
所以g(x)是奇函数
(II)g′(x)=
令g′(x)=0得x=
x∈(1,
)时,g′(x)<0;x∈(
,4)时,g′(x)>0
∴x=
时,函数有最小值
当x=1时,g(1)=
;x=4时,g(4)=
>
∴函数g(x)在区间[1,4]上的最大值为
和最小值为
.
g(-x)=
| 1 |
| 2 |
| 2 |
| x |
| 1 |
| 2 |
| 2 |
| x |
所以g(x)是奇函数
(II)g′(x)=
| 1 |
| 2 |
| x2-2 |
| x2 |
令g′(x)=0得x=
| 2 |
x∈(1,
| 2 |
| 2 |
∴x=
| 2 |
| 2 |
当x=1时,g(1)=
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
∴函数g(x)在区间[1,4]上的最大值为
| 9 |
| 4 |
| 2 |
点评:本题考查判断函数奇偶性的步骤、考查利用导数研究函数的单调性、极值、最值.

练习册系列答案
相关题目
 ,则f(0)= .
,则f(0)= .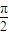 x+2ψ)(0<ψ<
x+2ψ)(0<ψ<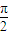 )的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )
)的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )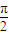 x+2ψ)(0<ψ<
x+2ψ)(0<ψ<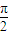 )的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )
)的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )