题目内容
已知点P是圆x2+y2=4上一动点,定点Q(4,0).(1)求线段PQ中点的轨迹方程;
(2)设∠POQ的平分线交PQ于R,求R点的轨迹方程.
解：（1）设PQ中点M(x,y),则P(2x-4,2y)，代入圆的方程得(x-2)2+y2=1.
（2）设R(x,y),由
=
=
，
设P(m,n),则有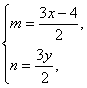
代入x2+y2=4中，得
(x-
)2+y2=
(y≠0).
练习册系列答案
相关题目
题目内容
已知点P是圆x2+y2=4上一动点,定点Q(4,0).(1)求线段PQ中点的轨迹方程;
(2)设∠POQ的平分线交PQ于R,求R点的轨迹方程.
解：（1）设PQ中点M(x,y),则P(2x-4,2y)，代入圆的方程得(x-2)2+y2=1.
（2）设R(x,y),由==，
设P(m,n),则有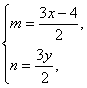
代入x2+y2=4中，得
(x-)2+y2=(y≠0).
的点M的轨迹为曲线C．
的点M的轨迹为曲线C．