题目内容
点P为直线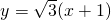 上任意一点,点A(0,0),B(3,0),则∠APB的最大值为________.
上任意一点,点A(0,0),B(3,0),则∠APB的最大值为________.

分析:设经过A、B两点的圆为圆M,且圆M直线
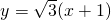 相切于点P0,根据平面几何知识可得:当动点P与点P0重合时,∠APB的最大.然后设出圆M方程为:x2+y2+Dx+Ey+F=0,利用点A(0,0)和B(3,0)在圆M上,解出D=-3且F=0,再利用圆心到直线
相切于点P0,根据平面几何知识可得:当动点P与点P0重合时,∠APB的最大.然后设出圆M方程为:x2+y2+Dx+Ey+F=0,利用点A(0,0)和B(3,0)在圆M上,解出D=-3且F=0,再利用圆心到直线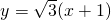 的距离等于半径解出E的值,从而得到圆M的方程.最后联解直线
的距离等于半径解出E的值,从而得到圆M的方程.最后联解直线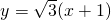 与圆M的方程,得到切点P0坐标为(0,
与圆M的方程,得到切点P0坐标为(0, ),在Rt△P0AB中利用正切定义求出最大角为
),在Rt△P0AB中利用正切定义求出最大角为 .
.解答:如图,作出经过A、B两点的圆M,且圆M直线
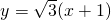 相切于点P0,
相切于点P0,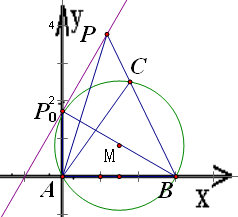
动在直线
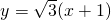 上运动,则点P与点P0重合时,∠APB的最大.
上运动,则点P与点P0重合时,∠APB的最大.证明如下:当点P位于圆M外时,设PB交圆M于点C,
连接AC,则∠AP0B=∠ACB>∠APB,所以∠AP0B是∠APB的最大值.
设圆M方程为:x2+y2+Dx+Ey+F=0,据题意得:
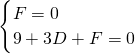 ?D=-3且F=0
?D=-3且F=0∴圆M方程为:x2+y2-3x+Ey=0,圆心M(
 ,-
,-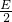 ),半径为
),半径为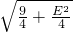
∵圆M直线
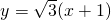 相切,即与直线
相切,即与直线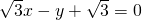 相切,
相切,∴
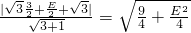 ?E=-
?E=- ,
,所以,圆M方程为:x2+y2-3x-
 y=0,再由
y=0,再由 联解,得
联解,得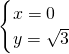 ,所以点P0坐标为(0,
,所以点P0坐标为(0, ).
).此时,在Rt△P0AB中有tan∠AP0B=
 =
=
∴∠AP0B=
 ,即∠APB的最大值为
,即∠APB的最大值为
故答案为:

点评:本题借助于一个动点到两个定点的张角的最大值的问题为载体,着重考查了直线与圆的位置关系和三角函数的基本概念等知识点,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 (a>b>0)的右焦点交椭圆于A.B两
(a>b>0)的右焦点交椭圆于A.B两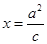 上任意一点,则∠APB为 ( )
上任意一点,则∠APB为 ( ) 上任意一点,点A(0,0),B(3,0),则∠APB的最大值为 .
上任意一点,点A(0,0),B(3,0),则∠APB的最大值为 .