Question

如图，在四棱锥P—ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC,E是PC的中点，作EF⊥PB交PB于点F.

 

(1)求证：PA∥平面EDB；

(2)求证：PB⊥平面EFD；

(3)求二面角C-PB-D的大小.

Answer 1

思路解析：本题涉及的问题包括：判定直线与平面平行和垂直，计算二面角的大小.这些问题都可以利用向量方法解决.由于已知条件中四棱锥的底面是正方形，一条侧棱垂直于底面，所以非常适合建立空间直角坐标系表示向量.

解：如题图，建立空间直角坐标系，点D为坐标原点，设DC=1.

(1)证明：连结AC交BD于点G，连结EG.

依题意，得A(1,0,0),P(0,0,1),E(0,,).

因为底面ABCD是正方形，所以点G是此正方形的中心，故点G的坐标为(,,0)，且=(1,0,-1), =(,0,-),所以=2,即∥.

而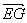平面EDB,且PA平面EDB，因此PA∥平面EDB.

(2)证明：依题意，得B(1,1,0),PB=(1,1,-1).

又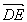=(0,,),故·=0+-=0,所以PB⊥DE.

由已知EF⊥PB，且EF∩DE=E,所以PB⊥平面EFD.

(3)解：已知PB⊥EF，由(2)可知PB⊥DF，故∠EFD是二面角C-PB-D的平面角.

设点F的坐标为(x,y,z)，则=(x,y,z-1).

因为=k，所以(x,y,z-1)=k(1,1,-1)=(k,k,-k)，

即x=k,y=k,z=1-k.

因为·=0,所以(1,1,-1)·(k,k,1-k)=k+k-1+k=3k-1=0.

所以k=，点F的坐标为(,,).

又点E的坐标为(0,,)，所以FE=(-,,-).

因为cos∠EFD=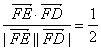,所以∠EFD=60°,即二面角C-PB-D的大小为60°.

方法归纳  建立坐标系，将向量坐标化，然后进行坐标形式下的向量运算，是本例的基本解题思路.解题的关键是确定关键点的坐标(位置)，这好似战斗中占据制高点非常重要一样.