题目内容
（2012•天门模拟）已知函数f(x)=
sinωx-2sin2
(ω＞0)的最小正周期为3π．
（Ⅰ）求函数f（x）的表达式；
（Ⅱ）在△ABC中，a，b，c分别为角A，B，C所对的边，且a＜b＜c，
a=2csinA；求角C的大小；
（Ⅲ）在（Ⅱ）的条件下，若f(
A+
)=
，求cosB的值．
| 3 |
| ωx |
| 2 |
（Ⅰ）求函数f（x）的表达式；
（Ⅱ）在△ABC中，a，b，c分别为角A，B，C所对的边，且a＜b＜c，
| 3 |
（Ⅲ）在（Ⅱ）的条件下，若f(
| 3 |
| 2 |
| π |
| 2 |
| 11 |
| 13 |
分析：（Ⅰ）利用二倍角公式、两角和的直线函数化简函数为一个角的一个三角函数的形式，即可得到函数f（x）的表达式；
（Ⅱ）通过正弦定理利用
a=2csinA，求出sinC的值，结合a＜b＜c，求角C的大小；
（Ⅲ）在（Ⅱ）的条件下，利用f(
A+
)=
，求出sinA，cosA，然后求出cosB的值．
（Ⅱ）通过正弦定理利用
| 3 |
（Ⅲ）在（Ⅱ）的条件下，利用f(
| 3 |
| 2 |
| π |
| 2 |
| 11 |
| 13 |
解答：解：（Ⅰ）f(x)=
sinωx-2sin2
=
sinωx-2•
=2sin（ωx+
）-1
函数f(x)=
sinωx-2sin2
(ω＞0)的最小正周期为3π．
即：
=3π，解得ω=
．
（Ⅱ）因为
a=2csinA
∴
=
=
又sinA≠0，∴sinC=
又因为a＜b＜c，所以C=
．
（Ⅲ）f(
A+
)=
，⇒cosA=
∵0＜A＜
∴sinA=
=
∴cosB=cos（
-A）=cos
cosA+sin
sinA
=
| 3 |
| ωx |
| 2 |
| 3 |
| 1-cosωx |
| 2 |
=2sin（ωx+
| π |
| 6 |
函数f(x)=
| 3 |
| ωx |
| 2 |
即：
| 2π |
| ω |
| 2 |
| 3 |
（Ⅱ）因为
| 3 |
∴
| a |
| c |
| 2sinA | ||
|
| sinA |
| sinC |
又sinA≠0，∴sinC=
| ||
| 2 |
又因为a＜b＜c，所以C=
| 2π |
| 3 |
（Ⅲ）f(
| 3 |
| 2 |
| π |
| 2 |
| 11 |
| 13 |
| 12 |
| 13 |
∵0＜A＜
| π |
| 3 |
| 1-cos2A |
| 5 |
| 13 |
∴cosB=cos（
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=
12+5
| ||
| 26 |
点评：本题考查三角函数的化简求值，三角函数公式的灵活运应，注意解答范围与三角形边的关系，考查计算能力，常考题型．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
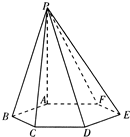（2012•天门模拟）已知如图，六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC．则下列结论正确的个数是（ ）