Question

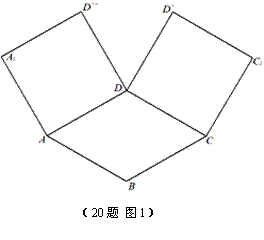
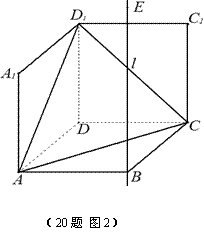
（本小题满分12分）如图1，在平面内，ABCD边长为2的正方形，和都是正方形。将两个正方形分别沿AD，CD折起，使与重合于点D₁。设直线l过点B且垂直于正方形ABCD所在的平面，点E是直线l上的一个动点，且与点D₁位于平面ABCD同侧，设（图2）。

（1）设二面角E – AC – D₁的大小为q ，当时，求的余弦值；

（2）当时在线段上是否存在点，使平面平面，若存在，求出分所成的比；若不存在，请说明理由。

Answer 1

解：（1）连接DB交AC于点O，连接DO，EO。在中，AD=DC

，同理可证：

为所求二面角的平面角。_{………3分}

在中，。

同理可得：。.

所以在中，有余弦定理得到，

cos=。                  _{………………6分}

_{注：坐标法以例给分。}

（2）设以D为原点，对DA，DC,DD₁所在直线分别为x,y,z轴，建立空间直角坐标系如图所示。BE = t  (t>2).

，E(2,2,t) _…7分

_{………9分}

设平面的法向量

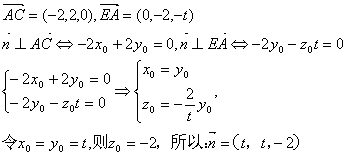                                                    _{……………………10分}

由平面平面，得平面，

    _{……………………11分}

所以：在线段上是存在点，使平面平面，分所成的比                                       k*s*5u_{………………12分}

_{注：几何法以例给分}