题目内容
(本题满分12分)已知 ,
,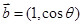 ,
,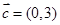 ,
,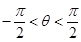 .
.
(1)若 ,求
,求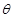 ;
;
(2)求 的取值范围;
的取值范围;
 ,
,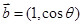 ,
,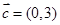 ,
,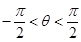 .
.(1)若
 ,求
,求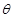 ;
;(2)求
 的取值范围;
的取值范围;(1)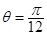 或
或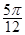 . (2) |a+b|
. (2) |a+b|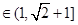 .
.
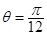 或
或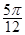 . (2) |a+b|
. (2) |a+b|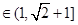 .
.本试题主要是考查了向量共线以及向量的数量积性质的综合运用。
(1)因为4a-c=(4sin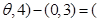 4sin
4sin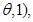 ∵(4a-c)∥b,∴4sin
∵(4a-c)∥b,∴4sin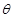 cos
cos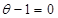 .∴sin
.∴sin ,进而解得。
,进而解得。
(2)a+b=(sin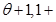 cos
cos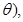 |a+b|
|a+b|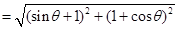 ,转换为三角函数,利用三角函数的性质得到范围。
,转换为三角函数,利用三角函数的性质得到范围。
(1)4a-c=(4sin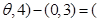 4sin
4sin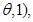 ……………2分
……………2分
∵(4a-c)∥b,∴4sin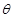 cos
cos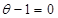 .∴sin
.∴sin . ……………4分
. ……………4分
∵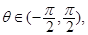 ∴
∴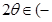
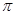 ,
,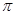 ). ∴
). ∴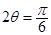 或
或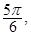 即
即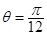 或
或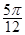 . ………6分
. ………6分
(2)a+b=(sin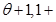 cos
cos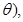 |a+b|
|a+b|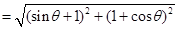 …………………2分
…………………2分
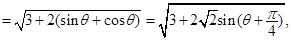 …………………3分
…………………3分
∵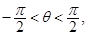 ∴
∴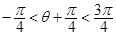 . ∴sin
. ∴sin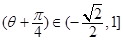 .
.
∴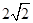 sin
sin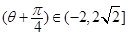 . ……………5分
. ……………5分
∴|a+b|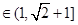 . …………………6分
. …………………6分
(1)因为4a-c=(4sin
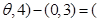 4sin
4sin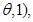 ∵(4a-c)∥b,∴4sin
∵(4a-c)∥b,∴4sin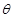 cos
cos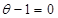 .∴sin
.∴sin ,进而解得。
,进而解得。(2)a+b=(sin
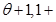 cos
cos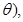 |a+b|
|a+b|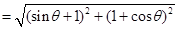 ,转换为三角函数,利用三角函数的性质得到范围。
,转换为三角函数,利用三角函数的性质得到范围。(1)4a-c=(4sin
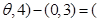 4sin
4sin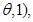 ……………2分
……………2分∵(4a-c)∥b,∴4sin
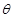 cos
cos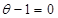 .∴sin
.∴sin . ……………4分
. ……………4分∵
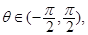 ∴
∴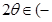
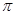 ,
,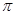 ). ∴
). ∴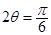 或
或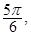 即
即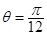 或
或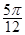 . ………6分
. ………6分(2)a+b=(sin
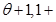 cos
cos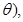 |a+b|
|a+b|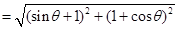 …………………2分
…………………2分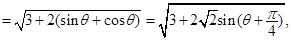 …………………3分
…………………3分∵
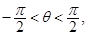 ∴
∴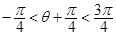 . ∴sin
. ∴sin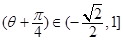 .
. ∴
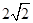 sin
sin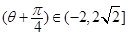 . ……………5分
. ……………5分∴|a+b|
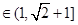 . …………………6分
. …………………6分
练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 的三个内角
的三个内角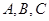 所对的边分别为a,b,c,向量
所对的边分别为a,b,c,向量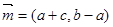 ,
,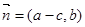 ,且
,且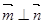 .
.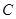 的大小;
的大小;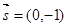 ,
,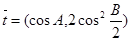 ,试求
,试求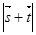 的取值范围
的取值范围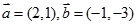 ,则
,则 等于
等于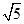 C.
C.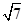
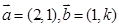 且
且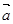 与
与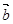 的夹角为锐角,则
的夹角为锐角,则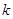 的取值范围是( )
的取值范围是( )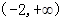 B.
B.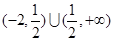 C .
C .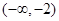 D.
D.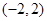
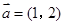 ,
,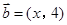 ,若向量
,若向量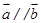 ,则
,则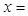 ( )
( )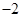
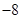
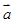 ,
,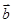 的夹角为
的夹角为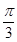 ,那么
,那么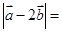 .
.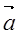 =(1,2),
=(1,2),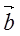 =(x,1),若
=(x,1),若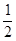
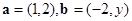 ,若
,若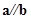 ,则
,则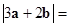
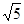
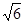
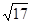
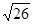
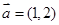 ,
,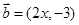 ,若
,若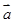 ∥
∥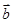 ,则
,则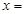 ( )
( )