题目内容
(2011•渭南三模)已知等差数列{an}的前n项和为Sn,且a3=5,S15=225.
(Ⅰ)求数列{an}的通项an;
(Ⅱ)设bn=
×2an+
,求数列{bn}的前n项和Tn..
(Ⅰ)求数列{an}的通项an;
(Ⅱ)设bn=
| 3 |
| 2 |
| 1 |
| n(n+1) |
分析:(Ⅰ)设出等差数列的首项和等差,根据等差数列的通项公式及前n项和的公式把已知条件a3=5,S15=225化简,得到关于首项和公差的两个关系式,联立两个关系式即可求出首项和公差,根据首项和公差写出数列的通项公式即可;
(Ⅱ)现对{bn}的通项变形可得,bn=
×22n-1+(
-
),用分组求和法,可得Tn=
×(21+23+25+…+22n-1)+(1-
)+(
-
)+…+(
-
),前一部分用等比数列的前n项和公式计算,后一部分用错位相减法,计算可得答案.
(Ⅱ)现对{bn}的通项变形可得,bn=
| 3 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
解答:解:(Ⅰ)设等差数列{an}首项为a1,公差为d,
由题意,得
,
解得
,
∴an=2n-1;
(Ⅱ)bn=
×2an+
=
×22n-1+(
-
),
Tn=b1+b2+b3+…+bn=
×(21+23+25+…+22n-1)+(1-
)+(
-
)+…+(
-
)=
(
)+(1-
)=3×2n-2,
由题意,得
|
解得
|
∴an=2n-1;
(Ⅱ)bn=
| 3 |
| 2 |
| 1 |
| n(n+1) |
| 3 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
Tn=b1+b2+b3+…+bn=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 3 |
| 2 |
| 2(1-2n) |
| 1-2 |
| 1 |
| n+1 |
点评:此题考查等差数列的通项公式及数列的求和,关键是灵活运用分组求和法求Tn的值.

练习册系列答案
相关题目
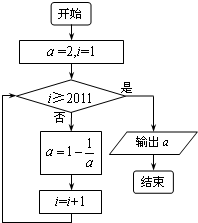 (2011•渭南三模)已知某程序框图如图所示,则执行该程序后输出的结果是( )
(2011•渭南三模)已知某程序框图如图所示,则执行该程序后输出的结果是( ) (2011•渭南三模)已知正三棱柱的侧面积为36,其三视图如图所示,则它的左视图的面积为( )
(2011•渭南三模)已知正三棱柱的侧面积为36,其三视图如图所示,则它的左视图的面积为( )