题目内容
设a∈R,函数f(x)=lnx-ax.
(1)若a=2,求曲线y=f(x)在P(1,-2)处的切线方程;
(2)若f(x)无零点,求实数a的取值范围;
(3)若f(x)有两个相异零点x1,x2,求证:x1•x2>e2.
解:在区间(0,+∞)上, .…(1分)
.…(1分)
(1)当a=2时,f′(1)=1-2=-1,则切线方程为y-(-2)=-(x-1),即x+y+1=0 …(3分)
(2)①若a<0,则f′(x)>0,f(x)是区间(0,+∞)上的增函数,
∵f(1)=-a>0,f(ea)=a-aea=a(1-ea)<0,
∴f(1)•f(ea)<0,函数f(x)在区间(0,+∞)有唯一零点.…(6分)
②若a=0,f(x)=lnx有唯一零点x=1.…(7分)
③若a>0,令f′(x)=0得: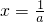 .
.
在区间(0, )上,f′(x)>0,函数f(x)是增函数;
)上,f′(x)>0,函数f(x)是增函数;
在区间( ,+∞)上,f′(x)<0,函数f(x)是减函数;
,+∞)上,f′(x)<0,函数f(x)是减函数;
故在区间(0,+∞)上,f(x)的极大值为f( )=
)= .
.
由于f(x)无零点,须使 ,解得:
,解得: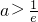 .
.
故所求实数a的取值范围是( ,+∞).…(9分)
,+∞).…(9分)
(3)设x1>x2>0,∵f(x1)=0,f(x2)=0,∴lnx1-ax1=0,lnx2-ax2=0,
∴lnx1-lnx2=a(x1-x2),lnx1+lnx2=a(x1+x2)
原不等式x1•x2>e2等价于lnx1+lnx2>2?a(x1+x2)>2? ?
?
令 ,则t>1,于是
,则t>1,于是 ?
? .…(12分)
.…(12分)
设函数 ,
,
求导得: ,
,
故函数g(t)是(1,+∞)上的增函数,∴g(t)>g(1)=0
即不等式 成立,故所证不等式x1•x2>e2成立.…(14分)
成立,故所证不等式x1•x2>e2成立.…(14分)
分析:(1)先确定函数f(x)的定义域,然后对函数f(x)求导,根据导函数求出f′(1)=-1,得到切线方程.
(2)当a≤0时,函数有零点;当a>0时,极大值小于0,函数没有零点,由此可求实数a的取值范围.
(3)由于f(x)有两个相异零点x1,x2,可知f(x1)=0,f(x2)=0,再原不等式x1•x2>e2进一步整理得到 ,只要能证出上述不等式恒成立即可.
,只要能证出上述不等式恒成立即可.
点评:本题主要考查了导数在函数单调性和函数极值中的应用,连续函数的零点存在性定理及其应用,分类讨论的思想方法,属中档题
 .…(1分)
.…(1分)(1)当a=2时,f′(1)=1-2=-1,则切线方程为y-(-2)=-(x-1),即x+y+1=0 …(3分)
(2)①若a<0,则f′(x)>0,f(x)是区间(0,+∞)上的增函数,
∵f(1)=-a>0,f(ea)=a-aea=a(1-ea)<0,
∴f(1)•f(ea)<0,函数f(x)在区间(0,+∞)有唯一零点.…(6分)
②若a=0,f(x)=lnx有唯一零点x=1.…(7分)
③若a>0,令f′(x)=0得:
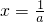 .
.在区间(0,
 )上,f′(x)>0,函数f(x)是增函数;
)上,f′(x)>0,函数f(x)是增函数;在区间(
 ,+∞)上,f′(x)<0,函数f(x)是减函数;
,+∞)上,f′(x)<0,函数f(x)是减函数;故在区间(0,+∞)上,f(x)的极大值为f(
 )=
)= .
.由于f(x)无零点,须使
 ,解得:
,解得: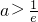 .
.故所求实数a的取值范围是(
 ,+∞).…(9分)
,+∞).…(9分)(3)设x1>x2>0,∵f(x1)=0,f(x2)=0,∴lnx1-ax1=0,lnx2-ax2=0,
∴lnx1-lnx2=a(x1-x2),lnx1+lnx2=a(x1+x2)
原不等式x1•x2>e2等价于lnx1+lnx2>2?a(x1+x2)>2?
 ?
?
令
 ,则t>1,于是
,则t>1,于是 ?
? .…(12分)
.…(12分)设函数
 ,
,求导得:
 ,
,故函数g(t)是(1,+∞)上的增函数,∴g(t)>g(1)=0
即不等式
 成立,故所证不等式x1•x2>e2成立.…(14分)
成立,故所证不等式x1•x2>e2成立.…(14分)分析:(1)先确定函数f(x)的定义域,然后对函数f(x)求导,根据导函数求出f′(1)=-1,得到切线方程.
(2)当a≤0时,函数有零点;当a>0时,极大值小于0,函数没有零点,由此可求实数a的取值范围.
(3)由于f(x)有两个相异零点x1,x2,可知f(x1)=0,f(x2)=0,再原不等式x1•x2>e2进一步整理得到
 ,只要能证出上述不等式恒成立即可.
,只要能证出上述不等式恒成立即可.点评:本题主要考查了导数在函数单调性和函数极值中的应用,连续函数的零点存在性定理及其应用,分类讨论的思想方法,属中档题

练习册系列答案
相关题目
设a∈R,函数f(x)=ex-ae-x的导函数为f′(x),且f′(x)是奇函数,则a=( )
| A、0 | B、1 | C、2 | D、-1 |