题目内容

设实数a，b满足
2a-b+1≥0
2a+b-4≥0
2a≤3
，则4a2+b2的最大值是（　　）
A、25
B、50
C、1
D、
25
3
分析：本题考查的知识点是简单线性规划的应用，我们要先画出满足约束条件
2a-b+1≥0
2a+b-4≥0
2a≤3
的平面区域，然后分析平面区域里各个角点，然后将其代入4a2+b2中，求出4a2+b2的最大值
解答：精英家教网解：满足约束条件
2a-b+1≥0
2a+b-4≥0
2a≤3
的平面区域如下图示：
由图可知，当a=
3
2
，b=4时，
4a2+b2有最大值25
故选A
点评：平面区域的最值问题是线性规划问题中一类重要题型，在解题时，关键是正确地画出平面区域，分析表达式的几何意义，然后结合数形结合的思想，分析图形，找出满足条件的点的坐标，即可求出答案．
练习册系列答案
相关题目
（2012•福建模拟）（1）选修4-2：矩阵与变换
已知向量
1
-1
在矩阵M=
1m
01
变换下得到的向量是
0
-1
．
（Ⅰ）求m的值；
（Ⅱ）求曲线y2-x+y=0在矩阵M-1对应的线性变换作用下得到的曲线方程．
（2）选修4-4：极坐标与参数方程
在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系．已知点M的极坐标为(4
2
，
π
4
)，曲线C的参数方程为
x=1+
2
cosα
y=
2
sinα
（α为参数）．
（Ⅰ）求直线OM的直角坐标方程；
（Ⅱ）求点M到曲线C上的点的距离的最小值．
（3）选修4-5：不等式选讲
设实数a，b满足2a+b=9．
（Ⅰ）若|9-b|+|a|＜3，求a的取值范围；
（Ⅱ）若a，b＞0，且z=a2b，求z的最大值．
（2012•福建模拟）（1）选修4-2：矩阵与变换
已知向量
1
-1
在矩阵M=
1m
01
变换下得到的向量是
0
-1
．
（Ⅰ）求m的值；
（Ⅱ）求曲线y2-x+y=0在矩阵M-1对应的线性变换作用下得到的曲线方程．
（2）选修4-4：极坐标与参数方程
在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系．已知点M的极坐标为（4
2
，
π
4
），曲线C的参数方程为
x=1+
2
cosα
y=
2
sinα
（α为参数）．
（Ⅰ）求直线OM的直角坐标方程；
（Ⅱ）求点M到曲线C上的点的距离的最小值．
（3）选修4-5：不等式选讲
设实数a、b满足2a+b=9．
（Ⅰ）若|9-b|+|a|＜3，求x的取值范围；
（Ⅱ）若a，b＞0，且z=a2b，求z的最大值．
（1）选修4-2：矩阵与变换
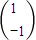已知向量在矩阵M=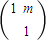变换下得到的向量是．
（Ⅰ）求m的值；
（Ⅱ）求曲线y2-x+y=0在矩阵M-1对应的线性变换作用下得到的曲线方程．
（2）选修4-4：极坐标与参数方程
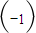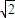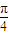在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系．已知点M的极坐标为（4，），曲线C的参数方程为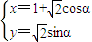（α为参数）．
（Ⅰ）求直线OM的直角坐标方程；
（Ⅱ）求点M到曲线C上的点的距离的最小值．
（3）选修4-5：不等式选讲
设实数a、b满足2a+b=9．
（Ⅰ）若|9-b|+|a|＜3，求x的取值范围；
（Ⅱ）若a，b＞0，且z=a2b，求z的最大值．
（1）选修4-2：矩阵与变换
已知向量在矩阵变换下得到的向量是．
（Ⅰ）求m的值；
（Ⅱ）求曲线y2-x+y=0在矩阵M-1对应的线性变换作用下得到的曲线方程．
（2）选修4-4：极坐标与参数方程
在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系．已知点M的极坐标为，曲线C的参数方程为（α为参数）．
（Ⅰ）求直线OM的直角坐标方程；
（Ⅱ）求点M到曲线C上的点的距离的最小值．
（3）选修4-5：不等式选讲
设实数a，b满足2a+b=9．
（Ⅰ）若|9-b|+|a|＜3，求a的取值范围；
（Ⅱ）若a，b＞0，且z=a2b，求z的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网