题目内容
18.如图,在直三棱柱(I)证明:![]() ;
;
(II)求![]() 的长,并求点
的长,并求点![]() 到平面
到平面![]() 的距离.
的距离.
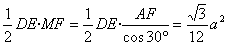
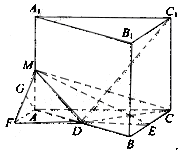
(I)证明:连结CD.
∵三棱柱ABC—A1B1C1是直三棱柱,
∴CC1⊥平面ABC,
∴CD为C1D在平面ABC内的射影.
∵△ABC中,AC=BC,D为AB中点,
∴AB⊥CD,
∴AB⊥C1D,
∵A1B1∥AB,
∴A1B1⊥C1D.
(II)解法一:过A点作CE的平行线,交ED的延长线于F,连结MF.
∵D、E分别为AB、BC的中点,
∴DE∥AC,
又∵AF∥CE,CE⊥AC,
∴AF⊥DE.
∵MA⊥平面ABC.
∴AF为MF在平面ABC内的射影,
∴MF⊥DE,
∴∠MFA为二面角M—DE—A的平面角,∠MFA=30°.
在Rt△MAF中,AF=![]() BC=
BC=![]() ,∠MFA=30°,
,∠MFA=30°,
∴AM=![]() .
.
作AG⊥MF,垂足为G.
∵MF⊥DE,AF⊥DE,
∴DE⊥平面AMF,
∴平面MDE⊥平面AMF,
∴AG⊥平面MDE.
在Rt△GAF中, ∠GFA=30°,AF=![]() ,
,
∴AG=![]() ,即A到平面MDE的距离为
,即A到平面MDE的距离为![]() .
.
∵CA∥DE, ∴CA∥平面MDE.
∴C到平面MDE的距离与A到平面MDE的距离相等,为![]() .
.
解法二:过点A作CE的平行线,交ED的延长线于F,连接MF,
∵D、E分别为AB、CB的中点,
∴DE∥AC,
又∵AF∥CE,CE⊥AC,
∴AF⊥DE.
∵MA⊥平面ABC,
∴AF为MF在平面ABC内的射影,
∴MF⊥DE,
∴∠MFA为二面角M—DE—A的平面角,∠MFA=30°.
在Rt△MAF中,AF=![]() ,∠MFA=30°,
,∠MFA=30°,
∴AM=![]() a.
a.
设C到平面MDE的距离为h.
∵![]() ,
,
∴![]()
S△CDE=![]()
S△MDE=![]() ,
,
∴![]()
∴h=![]() ,即C到平面MDE的距离为
,即C到平面MDE的距离为![]() .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案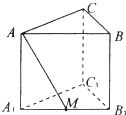 如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1=
如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1= 中, AB=1,
中, AB=1, ,
, .
. ;
; —B的正切值。
—B的正切值。
 中,
中, ,
, 分别为
分别为 的中点,四边形
的中点,四边形 是边长为
是边长为 的正方形.
的正方形. 平面
平面 ;
; 平面
平面 的余弦值.
的余弦值.
 中,
中, ,
, ,
, 是
是 的中点.
的中点. ∥平面
∥平面 ;
; 的余弦值;
的余弦值; 上是否存在点
上是否存在点 ,使
,使 与
与 成
成 角?若存在,确定
角?若存在,确定
 中,
中, ,点
,点 是
是 的中点.
的中点. ;(2)
;(2) 平面
平面 .
.