题目内容
据市场分析,粤西某海鲜加工公司,当月产量在10吨至25吨时,月生产总成本y(万元)可以看成月产量x(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本y(万元)关于月产量x(吨)的函数关系;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润;
(3)当月产量为多少吨时,每吨平均成本最低,最低成本是多少万元?
(1)写出月总成本y(万元)关于月产量x(吨)的函数关系;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润;
(3)当月产量为多少吨时,每吨平均成本最低,最低成本是多少万元?
分析:(1)设出函数解析式,代入(10,20),可得函数解析式;
(2)列出函数解析式,利用配方法,可求最大利润;
(3)求出每吨平均成本,利用基本不等式可求最值.
(2)列出函数解析式,利用配方法,可求最大利润;
(3)求出每吨平均成本,利用基本不等式可求最值.
解答:解:(1)由题意,设y=a(x-15)2+17.5(a∈R,a≠0)
将x=10,y=20代入上式得:20=25a+17.5,解得a=
,
∴y=
(x-15)2+17.5(10≤x≤25)
(2)设最大利润为Q(x),则Q(x)=1.6x-y=1.6x-(
x2-3x+40)=-
(x-23)2+12.9(10≤x≤25),因为x=23∈[10,25],所以月产量为23吨时,可获最大利润12.9万元.
(3)
=
=
x+
-3≥2
-3=1
当且仅当
=
,即x=20∈[10,25]时上式“=”成立.
故当月产量为20吨时,每吨平均成本最低,最低成本为1万元.
将x=10,y=20代入上式得:20=25a+17.5,解得a=
| 1 |
| 10 |
∴y=
| 1 |
| 10 |
(2)设最大利润为Q(x),则Q(x)=1.6x-y=1.6x-(
| 1 |
| 10 |
| 1 |
| 10 |
(3)
| y |
| x |
| ||
| x |
| 1 |
| 10 |
| 40 |
| x |
|
当且仅当
| x |
| 10 |
| 40 |
| x |
故当月产量为20吨时,每吨平均成本最低,最低成本为1万元.
点评:本题考查利用数学知识解决实际问题,考查基本不等式的运用,考查学生分析解决问题的能力,确定函数解析式是关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
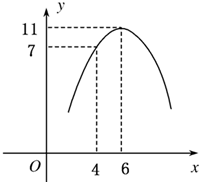 某汽车运输公司,购买一批客车投入营运,据市场分析,每辆客车营运的总利润y(单位:10万元)与营运年数x(x∈N*)的关系为二次函数(如图示),则每辆客车营运多少年,其营运的年平均利润最大,并求其最大值?
某汽车运输公司,购买一批客车投入营运,据市场分析,每辆客车营运的总利润y(单位:10万元)与营运年数x(x∈N*)的关系为二次函数(如图示),则每辆客车营运多少年,其营运的年平均利润最大,并求其最大值? 如图,某汽车运输公司刚买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润y(单位:10万元)与营运年数x(x∈N)为二次函数关系,若使营运的年平均利润最大,则每辆客车应营运( )
如图,某汽车运输公司刚买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润y(单位:10万元)与营运年数x(x∈N)为二次函数关系,若使营运的年平均利润最大,则每辆客车应营运( )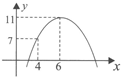 某汽车运输公司购买了-批豪华大客车投入客运,据市场分析,每辆客车营运的总利润y(万元)与营运年数x(x∈N*)为二次函数关系,如图所示,则每辆客车营运多少年使其营运年平均利润最大( )
某汽车运输公司购买了-批豪华大客车投入客运,据市场分析,每辆客车营运的总利润y(万元)与营运年数x(x∈N*)为二次函数关系,如图所示,则每辆客车营运多少年使其营运年平均利润最大( )