题目内容
已知函数
（其中
），且函数
的图象的相邻
两条对称轴间的距离为.
(1)先列表再作出函数
在区间
上的图象. (2)若
，求
的值；
(3)在△ABC中，角A，B，C的对边分别是a，b，c，且满足(2a－c)cosB＝bcosC，
求函数f(A)的取值范围。
解:(1)
=
=2
由条件得
，所以
，
…3分
(1)由(1)知，f(x)＝1＋2sin(x＋
)．列表：描点作图，函数f(x)在[－π，π]上的图象如图所示．
| x＋ | － | － | 0 |
| π |
|
| x | －π | － | － |
|
| π |
| y | 0 | －1 | 1 | 3 | 1 | 0 |
π
π
π
…………6分
（2）由可得sin(
＋
)＝
. ∴cos(
－x)＝cos(x－)
＝－cos(x＋
)＝－[1－2sin2(＋)]＝2·( )2－1＝－. …………9分
(3)∵(2a－c)cosB＝bcosC，
由正弦定理得(2sinA－sinC)cosB＝sinBcosC.∴2sinAcosB－cosBsinC＝sinBcosC，
∴2sinAcosB＝sin(B＋C)，∵A＋B＋C＝π，∴sin(B＋C)＝sinA，且sinA≠0，
∴cosB＝，B＝， ∴0＜A＜.∴＜A＋＜
，＜sin(A＋)≤1.
又∵f(x)＝2sin(＋)＋1，∴f(A)＝2sin(A＋)＋1
故函数f(A)的取值范围是(2，3 ]. …………14分
练习册系列答案
相关题目
，
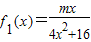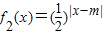其中m∈R且m≠o．
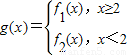当m≥2时，若对于任意的x1∈[2，+∞），总存在唯一的x2∈（-∞，2），使得g（x1）=g（x2）成立．试求m的取值范围．
，
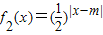其中m∈R且m≠o．
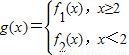当m≥2时，若对于任意的x1∈[2，+∞），总存在唯一的x2∈（-∞，2），使得g（x1）=g（x2）成立．试求m的取值范围．
，
其中m∈R且m≠o．
当m≥2时，若对于任意的x1∈[2，+∞），总存在唯一的x2∈（-∞，2），使得g（x1）=g（x2）成立．试求m的取值范围．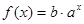
（其中
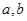为常量且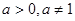
）的图像经过点
.
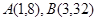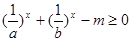在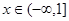
时恒成立，求实数
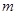的取值范围.
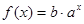（其中
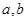为常量且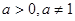
）的图像经过点
.
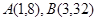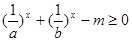在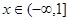
时恒成立，求实数
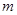的取值范围