题目内容
已知函数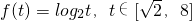
(1)求f(t)的值域G
(2)若对G内的所有实数x,不等式-x2+2mx-m2+2m≤1恒成立,求实数m的取值范围.
解:(1)∵函数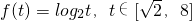 ,
,
∴ 即
即 ,
,
(2)-x2+2mx-m2+2m≤1恒成立?x2-2mx+m2-2m+1≥0恒成立,
令g(x)=x2-2mx+m2-2m+1
当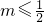 时
时 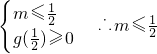
当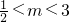 时
时 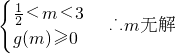
当m≥3时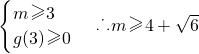
综上: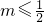 或
或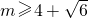 .
.
分析:(1)利用函数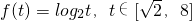 的单调性可求其值域G;
的单调性可求其值域G;
(2)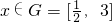 ,不等式-x2+2mx-m2+2m≤1恒成立可转化为x2-2mx+m2-2m+1≥0恒成立(
,不等式-x2+2mx-m2+2m≤1恒成立可转化为x2-2mx+m2-2m+1≥0恒成立( ),令g(x)=x2-2mx+m2-2m+1,其对称轴x=m,分区间在对称轴左侧(包括边界),右侧(包括边界),对称轴穿过
),令g(x)=x2-2mx+m2-2m+1,其对称轴x=m,分区间在对称轴左侧(包括边界),右侧(包括边界),对称轴穿过 ,三种情况利用函数的单调性及最值讨论解决.
,三种情况利用函数的单调性及最值讨论解决.
点评:本题考查函数恒成立问题,解决的关键是明确其对称轴在给定区间的什么位置,借助其单调性解决,属于中档题.
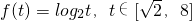 ,
,∴
 即
即 ,
,(2)-x2+2mx-m2+2m≤1恒成立?x2-2mx+m2-2m+1≥0恒成立,
令g(x)=x2-2mx+m2-2m+1
当
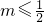 时
时 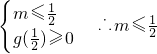
当
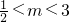 时
时 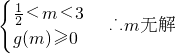
当m≥3时
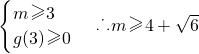
综上:
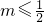 或
或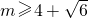 .
.分析:(1)利用函数
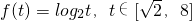 的单调性可求其值域G;
的单调性可求其值域G;(2)
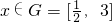 ,不等式-x2+2mx-m2+2m≤1恒成立可转化为x2-2mx+m2-2m+1≥0恒成立(
,不等式-x2+2mx-m2+2m≤1恒成立可转化为x2-2mx+m2-2m+1≥0恒成立( ),令g(x)=x2-2mx+m2-2m+1,其对称轴x=m,分区间在对称轴左侧(包括边界),右侧(包括边界),对称轴穿过
),令g(x)=x2-2mx+m2-2m+1,其对称轴x=m,分区间在对称轴左侧(包括边界),右侧(包括边界),对称轴穿过 ,三种情况利用函数的单调性及最值讨论解决.
,三种情况利用函数的单调性及最值讨论解决.点评:本题考查函数恒成立问题,解决的关键是明确其对称轴在给定区间的什么位置,借助其单调性解决,属于中档题.

练习册系列答案
相关题目


 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.

