题目内容
把一颗骰子投掷两次，记第一次出现的点数为a2，第二次出现的点数为b2（其中a＞0，b＞0）．
（Ⅰ）若记事件A“焦点在x轴上的椭圆的方程为
”，求事件A的概率；
（Ⅱ）若记事件B“离心率为2的双曲线的方程为
”，求事件B的概率．
解：（a，b）所有可能的情况共有6×6=36种（如下图）
（4分）
（Ⅰ）事件A表示“焦点在x轴上的椭圆”，方程表示焦点在x轴上的椭圆，则a2＞b2，
所以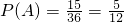
． （9分）
（Ⅱ）事件B表示“离心率为2的双曲线”，即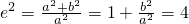
，
所以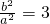
，则满足条件的有（1，3），（2，6），因此
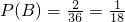．（13分）
分析：（a，b）所有可能的情况共有6×6=36种
（I）事件A“焦点在x轴上的椭圆的方程为”，即a＞b，找出符合条件的 事件的个数，代入古典概率的求解公式可求
（II）由e=2可得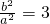，找出满足条件的事件的个数，代入古典概率的求解公式即可求解
点评：本题以圆锥曲线为载体，考查概率知识的运用，解题的关键是确定基本事件的个数．
| （1，1） | （1，2） | （1，3） | （1，4） | （1，5） | （1，6） |
| （2，1） | （2，2） | （2，3） | （2，4） | （2，5） | （2，6） |
| （3，1） | （3，2） | （3，3） | （3，4） | （3，5） | （3，6） |
| （4，1） | （4，2） | （4，3） | （4，4） | （4，5） | （4，6） |
| （5，1） | （5，2） | （5，3） | （5，4） | （5，5） | （5，6） |
| （6，1） | （6，2） | （6，3） | （6，4） | （6，5） | （6，6） |
（Ⅰ）事件A表示“焦点在x轴上的椭圆”，方程
表示焦点在x轴上的椭圆，则a2＞b2，所以
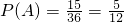． （9分）（Ⅱ）事件B表示“离心率为2的双曲线”，即
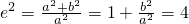，所以
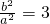，则满足条件的有（1，3），（2，6），因此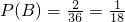．（13分）分析：（a，b）所有可能的情况共有6×6=36种
（I）事件A“焦点在x轴上的椭圆的方程为
”，即a＞b，找出符合条件的 事件的个数，代入古典概率的求解公式可求（II）由e=2可得
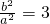，找出满足条件的事件的个数，代入古典概率的求解公式即可求解点评：本题以圆锥曲线为载体，考查概率知识的运用，解题的关键是确定基本事件的个数．
练习册系列答案
相关题目
（文）把一颗骰子投掷两次，第一次出现的点数记为a，第二次出现的点数记为b．已知直线l1：x+2y=2，直线l2：ax+by=4，则两直线l1、l2平行的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|