题目内容
从集合{1，2，3，…，11}中任选两个元素作为椭圆方程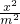
+
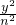=1中的m和n，则能组成落在矩形区域B={（x，y）||x|＜11，且|y|＜9}内的椭圆个数为
- A.43
- B.72
- C.86
- D.90
B
分析：首先确定m，n的取值，确定两种类型一是m，n都在1～8之间选值，一是m在9，10中选取，n在1～8中选取，求出椭圆数即可．
解答：椭圆落在矩形内，满足题意必须有，m≠n，所以有两类，
一类是m，n从{1，2，3，…6，7，8}任性两个不同数字，方法有A82=56
令一类是m从9，10，两个数字中选一个，n从{1，2，3，…6，7，8}中选一个
方法是：2×8=16
所以满足题意的椭圆个数是：56+16=72
故选B．
点评：本题考查二元一次不等式（组）与平面区域，椭圆的定义，组合知识，考查学生分析问题解决问题的能力．
分析：首先确定m，n的取值，确定两种类型一是m，n都在1～8之间选值，一是m在9，10中选取，n在1～8中选取，求出椭圆数即可．
解答：椭圆落在矩形内，满足题意必须有，m≠n，所以有两类，
一类是m，n从{1，2，3，…6，7，8}任性两个不同数字，方法有A82=56
令一类是m从9，10，两个数字中选一个，n从{1，2，3，…6，7，8}中选一个
方法是：2×8=16
所以满足题意的椭圆个数是：56+16=72
故选B．
点评：本题考查二元一次不等式（组）与平面区域，椭圆的定义，组合知识，考查学生分析问题解决问题的能力．
练习册系列答案
相关题目
