题目内容
已知二次函数f(x)=ax2+(2a-1)x+1在区间 上的最大值为3,求实数a的值.
上的最大值为3,求实数a的值.
解:因为二次函数f(x)在区间 上的最大值为3,
上的最大值为3,
所以必有 ,或f(2)=3,或
,或f(2)=3,或 .
.
(1)若 ,即1-
,即1- =3,解得
=3,解得 ,
,
此时抛物线开口向下,对称轴方程为x=-2,且 ,
,
故a= 不合题意;
不合题意;
(2)若f(2)=3,即4a+2(2a-1)+1=3,解得 ,
,
此时抛物线开口向上,对称轴方程为x=0,闭区间的右端点距离对称轴较远,
故 符合题意;
符合题意;
(3)若 ,即
,即 =3,解得
=3,解得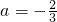 ,
,
此时抛物线开口向下,对称轴方程为x= ,闭区间的左端点距离对称轴较远,故
,闭区间的左端点距离对称轴较远,故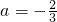 符合题意.
符合题意.
综上, 或
或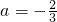 .
.
分析:由二次函数的性质可知:若f(x)在区间 上的最大值为3,则必有
上的最大值为3,则必有 ,或f(2)=3,或
,或f(2)=3,或 ,分情况求出a值,再加以验证即可.
,分情况求出a值,再加以验证即可.
点评:本题考查二次函数在闭区间上的最值,考查分类讨论思想、数形结合思想.
 上的最大值为3,
上的最大值为3,所以必有
 ,或f(2)=3,或
,或f(2)=3,或 .
.(1)若
 ,即1-
,即1- =3,解得
=3,解得 ,
,此时抛物线开口向下,对称轴方程为x=-2,且
 ,
,故a=
 不合题意;
不合题意;(2)若f(2)=3,即4a+2(2a-1)+1=3,解得
 ,
,此时抛物线开口向上,对称轴方程为x=0,闭区间的右端点距离对称轴较远,
故
 符合题意;
符合题意;(3)若
 ,即
,即 =3,解得
=3,解得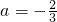 ,
,此时抛物线开口向下,对称轴方程为x=
 ,闭区间的左端点距离对称轴较远,故
,闭区间的左端点距离对称轴较远,故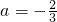 符合题意.
符合题意.综上,
 或
或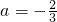 .
.分析:由二次函数的性质可知:若f(x)在区间
 上的最大值为3,则必有
上的最大值为3,则必有 ,或f(2)=3,或
,或f(2)=3,或 ,分情况求出a值,再加以验证即可.
,分情况求出a值,再加以验证即可.点评:本题考查二次函数在闭区间上的最值,考查分类讨论思想、数形结合思想.

练习册系列答案
相关题目