题目内容
设点F1是椭圆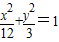
的左焦点，弦AB过椭圆的右焦点，则△F1AB的面积的最大值是（ ）A．6
B．12
C．
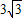
D．
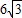
【答案】分析：设出直线AB的方程与椭圆的方程联立，得到根与系数的关系，再利用三角形的面积公式即可得出不等式，利用基本不等式的性质即可求出．
解答：解：设直线AB的方程为x=my+3，联立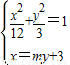
消去x得（m2+4）y2+6my-3=0．
设A（x1，y1），B（x2，y2）．则
．
．
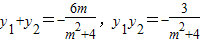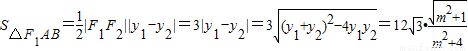令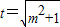
，则t≥1．
∴
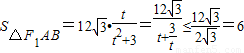．（当且仅当t=3时等号成立）
因此△F1AB的面积的最大值是6．
故选A．
点评：熟练掌握直线与椭圆相交问题的解题模式、根与系数的关系、基本不等式的性质是解题的关键．
解答：解：设直线AB的方程为x=my+3，联立
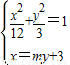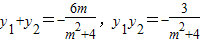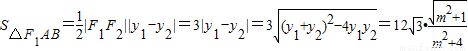消去x得（m2+4）y2+6my-3=0．设A（x1，y1），B（x2，y2）．则．．令
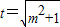，则t≥1．∴
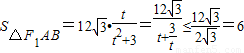．（当且仅当t=3时等号成立）因此△F1AB的面积的最大值是6．
故选A．
点评：熟练掌握直线与椭圆相交问题的解题模式、根与系数的关系、基本不等式的性质是解题的关键．
练习册系列答案
相关题目
=1（a＞b＞0）的左、右两个焦 点。（1）若椭圆C上的点A（1，
）到F1、F2两点的 距离之和等于4，写出椭圆C的方程和焦点坐标；