Question

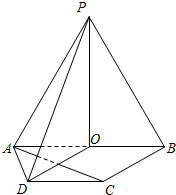
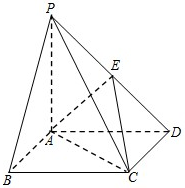
如图，在四棱锥P-ABCD中，底面ABCD为正方形，PA⊥平面ABCD，PA=AB，点E是PD的中点．
（1）求证：PB∥平面ACE；
（2）若四面体E-ACD的体积为

2

3

，求AB的长．

Answer 1

（1）证明：连接BD交AC于点O，连接EO，
∵ABCD是正方形
∴点O是BD的中点
又∵点E是PD的中点
∴EO是△DPB的中位线．
∴PB∥EO．
又∵EO?平面ACE，PB?平面ACE
∴PB∥平面ACE
（2）取AD的中点H，连接EH
∵点E是PD的中点
∴EH∥PA
又∵PA⊥平面ABCD
∴EH⊥平面ABCD．
设AB=x，则PA=AD=CD=x，且EH=

1

2

PA=

1

2

x．
所以VE-ACD=

1

3

S△ACD×EH=

1

3

×

1

2

×AD×CD×EH=

1

6

•x•x•

1

2

x=

1

12

x3=

2

3

解得x=2
故AB的长为2