题目内容
修建一个面积为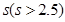 平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米.已知后面墙的造价为每米45元,其他墙的造价为每米180元,设后面墙长度为
平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米.已知后面墙的造价为每米45元,其他墙的造价为每米180元,设后面墙长度为 米,修建此矩形场地围墙的总费用为
米,修建此矩形场地围墙的总费用为 元.
元.
(1)求 的表达式;
的表达式;
(2)试确定 ,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
(1)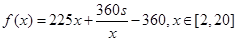 ;(2)若
;(2)若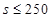 ,则当
,则当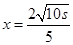 时
时
最小总费用为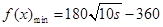 (元);若
(元);若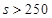 时,当
时,当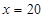 时,最小总费用为
时,最小总费用为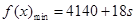 (元).
(元).
解析试题分析:(1)设矩形的另一边长为 米,依题意可得列出
米,依题意可得列出 的表达式(含
的表达式(含 ):
):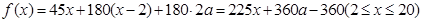 ,另一方面
,另一方面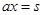 ,进而得到
,进而得到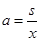 ,代入上式即可得到
,代入上式即可得到 的表达式(不含
的表达式(不含 );(2)先考虑函数
);(2)先考虑函数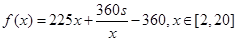 的单调性:
的单调性: 在
在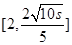 递减,在
递减,在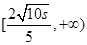 递增;进而针对
递增;进而针对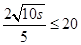 与
与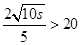 两种情况进行分类讨论,确定
两种情况进行分类讨论,确定 为何值时,总费用最低.
为何值时,总费用最低.
试题解析:(1)设矩形的另一边长为 米 1分
米 1分
则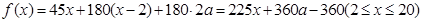 3分
3分
由已知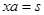 ,所以
,所以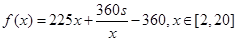 5分
5分
(2)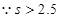 ,则
,则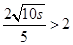 ,可以证明
,可以证明 在
在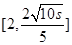 递减
递减
在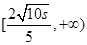 递增 7分
递增 7分
若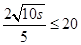 ,即
,即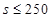 ,则当
,则当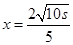 时
时
最小总费用为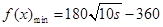 (元) 10分
(元) 10分
若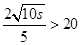 ,即
,即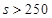 ,则当
,则当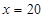 时,最小总费用为
时,最小总费用为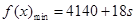 (元) 13分.
(元) 13分.
考点:函数的应用问题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
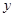 (万元)与处理量
(万元)与处理量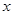 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: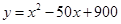 ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴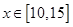 时,判断该项举措能否获利?如果能获利,求出最大利润;
时,判断该项举措能否获利?如果能获利,求出最大利润;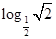 -log5
-log5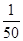 -log514;
-log514;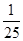 ×log3
×log3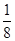 ×log5
×log5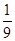 .
.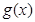 及二次函数
及二次函数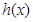 满足:
满足: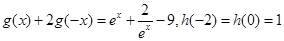 且
且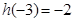 。
。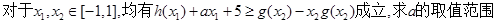 ;
;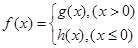 ,讨论方程
,讨论方程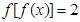 的解的个数情况.
的解的个数情况. 是
是 上的增函数,
上的增函数,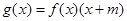 ,已知
,已知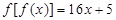 .
.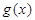 在
在 单调递增,求实数
单调递增,求实数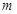 的取值范围;
的取值范围;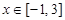 时,
时,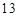 ,求实数
,求实数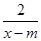 在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若p∧q为真,试求实数m的取值范围.
在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若p∧q为真,试求实数m的取值范围.