题目内容
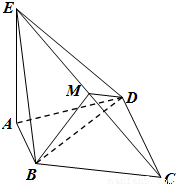
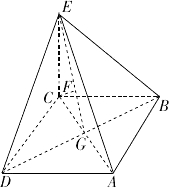 如图,四棱锥E-ABCD中,底面ABCD为正方形,EC⊥平面ABCD,AB=
如图,四棱锥E-ABCD中,底面ABCD为正方形,EC⊥平面ABCD,AB=| 2 |
(Ⅰ)求证:CF⊥平面BDE;
(Ⅱ)求二面角A-BE-D的大小.
分析:(Ⅰ)先用BD垂直于平面ACE证出CF⊥BD,在直角三角形ECG中证明CF⊥EG,即可由线面垂直的判定定理证明CF⊥平面BDE;
(Ⅱ)本题作二面角的平面角不易作出,但图形的结构易于建立空间坐标系,故建立如图的空间坐标系,求出两个平面的法向量由数量积公式求解二面角即可
(Ⅱ)本题作二面角的平面角不易作出,但图形的结构易于建立空间坐标系,故建立如图的空间坐标系,求出两个平面的法向量由数量积公式求解二面角即可
解答:解: (Ⅰ)证明:∵ABCD为正方形,AB=
(Ⅰ)证明:∵ABCD为正方形,AB=
,
∴AC=2,AC⊥BD,则CG=1=EC,
∵又F为EG中点,∴CF⊥EG.
∵EG⊥面ABCD,AC∩BD=G,BD⊥平面ECF,
∴CF⊥BDBD∩EG=G,∴CF⊥平面BDE (6分)
(Ⅱ)建立如图所示的空间直角坐标系C(0,0,0),F(
,
,
),B(0,
,0)[,A(
,
,0),E(0,0,1)
由(Ⅰ)知,
=(
,
,
)为平面BDE的一个法向量 (9分)
设平面ABE的法向量n=(x,y,z),
则n•
=0,n•
=0即
∴x=0且z=
y∴n=(0,1,
)(11分)
从而cos<n,
>=
=
∴二面角A-BE-D的大小为
.(13分)
 (Ⅰ)证明:∵ABCD为正方形,AB=
(Ⅰ)证明:∵ABCD为正方形,AB=| 2 |
∴AC=2,AC⊥BD,则CG=1=EC,
∵又F为EG中点,∴CF⊥EG.
∵EG⊥面ABCD,AC∩BD=G,BD⊥平面ECF,
∴CF⊥BDBD∩EG=G,∴CF⊥平面BDE (6分)
(Ⅱ)建立如图所示的空间直角坐标系C(0,0,0),F(
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
由(Ⅰ)知,
| CF |
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
设平面ABE的法向量n=(x,y,z),
则n•
| BA |
| BE |
|
∴x=0且z=
| 2 |
| 2 |
从而cos<n,
| CF |
n•
| ||
|n|•|
|
| ||
| 2 |
| π |
| 6 |
点评:本题考查用空间向量求平面间的夹角,求解本题的关键是建立空间坐标系,将两个平面的法向量求出,用数量积公式求解即可,空间向量求二面角其优势比较明显,建 系设标用公式,思路简单便于操作,比用几何法又要作图还要证明,思维量小了很多,但同时也可以发现用向量法做题,运算量偏大.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 (2012•西城区二模)如图,四棱锥E-ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
(2012•西城区二模)如图,四棱锥E-ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD. 如图,四棱锥 E-ABCD中,EA⊥平面ABCD,AB⊥AD,AB∥DC,AD=AE=CD=2AB,M是EC的中点.
如图,四棱锥 E-ABCD中,EA⊥平面ABCD,AB⊥AD,AB∥DC,AD=AE=CD=2AB,M是EC的中点.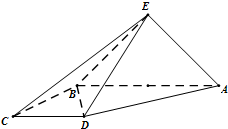 如图,四棱锥E-ABCD中,面ABE⊥面ABCD,
如图,四棱锥E-ABCD中,面ABE⊥面ABCD,