题目内容

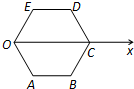（选修4-4：坐标系与参数方程）如图，边长为2的正六边形ABCDEO，以OC为极轴建立极坐标系，求CD边所在直线的极坐标方程．
分析：利用直角坐标方程的形式，先求出CD边所在直线的直角坐标方程，再利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即得CD边所在直线的直角坐标方程．
解答：解：CD边所在直线过C（4，0），且其倾斜角为
2π
3
，
故它的直角坐标方程为y=tan
2π
3
（x-4），即
3
x-4
3
+y=0，
利用ρcosθ=x，ρsinθ=y，进行代换，
即得CD边所在直线的直角坐标方程为：
3
ρcosθ+ρsinθ-4
3
=0．
点评：本小题主要考查直线的极坐标方程与直角坐标方程的互化等基本方法，属于基础题．
练习册系列答案
相关题目
本题（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分．
（1）选修4-2：矩阵与变换
已知矩阵A=
33
cd
，若矩阵A属于特征值6的一个特征向量为
α
=
1
1
，属于特征值1的一个特征向量为
β
=
^ 
&-2；
（Ⅰ）求矩阵A；
（Ⅱ）判断矩阵A是否可逆，若可逆求出其逆矩阵A-1．
（2）选修4-4：坐标系与参数方程
已知直线的极坐标方程为ρsin(θ+
π
4
)=
2
2
，圆M的参数方程为
x=2cosθ
y=-2+2sinθ
（其中θ为参数）．
（Ⅰ）将直线的极坐标方程化为直角坐标方程；
（Ⅱ）求圆M上的点到直线的距离的最小值．
（3）选修4-5：不等式选讲，设函数f（x）=|x-1|+|x-a|；
（Ⅰ）若a=-1，解不等式f（x）≥3；
（Ⅱ）如果关于x的不等式f（x）≤2有解，求a的取值范围．
A．选修4-1：几何证明选讲
如图，△ABC的外接圆的切线AE与BC的延长线相交于点E，∠BAC的平分线与BC
交于点D．求证：ED2=EB•EC．
B．选修4-2：矩阵与变换
求矩阵M=
-14
26
的特征值和特征向量．
C．选修4-4：坐标系与参数方程
在以O为极点的极坐标系中，直线l与曲线C的极坐标方程分别是ρcos(θ+
π
4
)=
3
2
2
和ρsin2θ=4cosθ，直线l与曲线C交于点．A，B，C，求线段AB的长．
D．选修4-5：不等式选讲
对于实数x，y，若|x-1|≤1，|y-2|≤1，求|x-y+1|的最大值．
选修4-4；坐标系与参数方程
在直角坐标系xOy中，直线L的参数方程为
x=3-
2
2
t
y=
2
2
t
（t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为ρ=2
5
sinθ．
（Ⅰ）求圆C的直角坐标方程；
（Ⅱ）设圆C与直线L交于点A，B，若点P的坐标为（3，
5
），求|PA|+|PB|．
（2012•许昌三模）选修4-4：坐标系与参数方程
在直角坐标系xoy中，直线l的参数方程为
x=a+4t
y=-1-2t
（t为参数）在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，极轴与x轴的非负半轴重合）中，圆C的方程为ρ=2
2
cos（θ+
π
4
）．
（Ⅰ）求圆心C到直线l的距离；
（Ⅱ）若直线l被圆C截得的弦长为
6
5
5
，求a的值．
（2013•广东模拟）（选修4-4：坐标系与参数方程选讲）
在直角坐标系xOy中，以原点O为极点，以x轴非负半轴为极轴，与直角坐标系xOy取相同的长度单位，建立极坐标系．设曲线C参数方程为
x=
3
cosθ
y= sinθ
（θ为参数），直线l的极坐标方程为ρcos(θ-
π
4
)=2
2
．则曲线C上的点到直线l的最大距离是
3
2
3
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网