题目内容
(2006
湖南,18)如下图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.(1)
证明:PQ⊥平面ABCD;(2)
求异面直线AQ与PB所成的角;(3)
求点P到平面QAD的距离.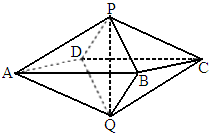
答案:略
解析:
解析:
|
解析: (1)连结AC、BD,设AC∩BD=O,因为P-ABCD与Q-ABCD都是正四棱锥,所以PO⊥平面ABCD,QO⊥平面AB-CD,从而P、O、Q三点在一条直线上,所以PQ⊥平面ABCD.(2) 由题设知,ABCD是正方形,所以AC⊥BD.由 (1)知,PQ⊥平面ABCD,故可分别以直线CA、DB、QP为x轴、y轴、z轴建立空间直角坐标系(如图),由题设条件,相关各点的坐标分别是P(0,0,1),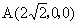 ,Q(0,0,-2), ,Q(0,0,-2), . .
所以  , ,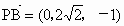 . .
于是 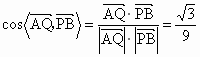 . .
从而异面直线 AQ与PB所成的角是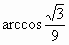 . .
(3) 由(2)知,点D的坐标是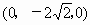 , ,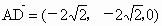 , ,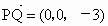 , ,
设 n=(x,y,z)是平面QAD的一个法向量,由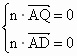 得 得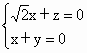 . .
取 x=1,得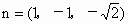 . .
所以点 P到平面QAD的距离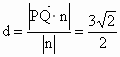 . . |

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
