题目内容
正方体AC1的棱长为a.
(1)求证:BD⊥平面ACC1A1;
(2)设P为D1D中点,求点P到平面ACC1A1的距离.
证明:(1)∵ AA1⊥AB,AA1⊥AD,且AB∩AD=A,
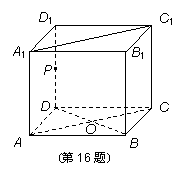 ∴ AA1⊥平面ABCD.
∴ AA1⊥平面ABCD.
又BD![]() 平面ABCD,∴ AA1⊥BD.
平面ABCD,∴ AA1⊥BD.
又AC⊥BD,AA1∩AC=A,∴ BD⊥平面ACC1A1.
(2)∵ DD1∥AA1,AA1![]() 平面ACC1A1,
平面ACC1A1,
∴ DD1∥平面ACC1A1.
∴ 点P到![]() 平面ACC1A1的距离即为直线DD1到面ACC1A1的距离. 也就是点D到平面ACC1A1的距离,设AC ∩BD=O,则DO的长度是点D到平面ACC1A1的距离.
平面ACC1A1的距离即为直线DD1到面ACC1A1的距离. 也就是点D到平面ACC1A1的距离,设AC ∩BD=O,则DO的长度是点D到平面ACC1A1的距离.
容易求出DO=![]() a.∴ P到平面A
a.∴ P到平面A![]() CC1A1的距离为
CC1A1的距离为![]() a.
a.

练习册系列答案
相关题目
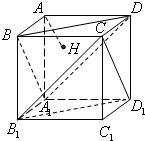 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有下列四个命题:
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有下列四个命题: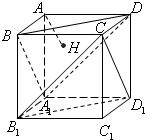
 如图,已知正方体AC1的棱长为1,求
如图,已知正方体AC1的棱长为1,求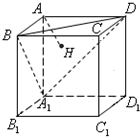 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则点H到平面A1B1C1D1 的距离为
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则点H到平面A1B1C1D1 的距离为