题目内容
在平面直角坐标系中，动点
到两条直线
与
的距离之和等于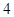
，则到原点距离的最小值为_________．
解析试题分析：本题考虑到两直线与相互垂直，且交点就是坐标原点，因此我们把这两条直线同时绕原点旋转到与坐标轴重合，在旋转过程中，动点到原点距离的最小值不变，这时动点变成到两坐标轴的距离这和为4，在第一象限内为线段
，到原点距离最小值为
，在其它三个象限也一样最小值为．这就是所求的最小值．（也可直接考虑，原点轨迹是一个边长为
的正方形，原点是正方形的中心）．
考点：轨迹问题与距离的最小值．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
，
之间的距离为
，则
.
被两平行线
所截得的线段的长为
，则直线
; ②
; ③ 
; ④
; ⑤
，
，则
、
两点的中点坐标为 
，给出下列四个命题：
；
如何变化,直线不过原点；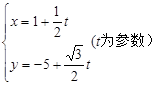
，另一条直线的方程是
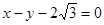，则两直线的交点与点
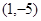间的距离是 ．