题目内容
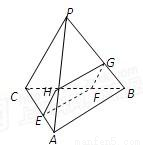
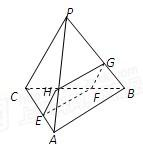如图，已知PO为正三棱锥P-ABC的高，AB=a，侧面与底面成α角，过O点作平面平行于PC和AB，得截面EFGH．（1）求证：PC⊥AB；
（2）截面EFGH的面积．
分析：（1）由三棱锥P-ABC为正棱锥和PO为正三棱锥P-ABC的高，则0为底面的中心，可知CO⊥AB，易得CO⊥平面PCO，可得到结论．
（2）如图所示：OK=
a，∠PKO=α，PK=
=
，侧棱为PA=
=
a，求得四边形的边长，又是矩形．最后由矩形面积求解．
（2）如图所示：OK=
| ||
| 6 |
| OK |
| cosα |
| ||
| 6cosα |
| PK2+AK2 |
| ||
| 6cosα |
解答：
解：（1）∵三棱锥P-ABC为正棱锥
∵PO为正三棱锥P-ABC的高
∴0为底面的中心
∴CO⊥AB
∴CO⊥平面PCO
∴PC⊥AB
（2）如图所示：OK=
a
又∵∠PKO=α
∴PK=
=
侧棱为：PA=
=
a
∴EF=
，EH=
a
又∵四边形EFGH为矩形
∴S四边形=
a2
解：（1）∵三棱锥P-ABC为正棱锥∵PO为正三棱锥P-ABC的高
∴0为底面的中心
∴CO⊥AB
∴CO⊥平面PCO
∴PC⊥AB
（2）如图所示：OK=
| ||
| 6 |
又∵∠PKO=α
∴PK=
| OK |
| cosα |
| ||
| 6cosα |
侧棱为：PA=
| PK2+AK2 |
| ||
| 6cosα |
∴EF=
| a |
| 2 |
| ||
| 12cosα |
又∵四边形EFGH为矩形
∴S四边形=
| ||
| 24cosα |
点评：本题主要考查三棱锥的结构特征，主要涉及了侧面与底面所成的角，四边形的形状及其相应量与棱锥的量的关系，属中档题．
练习册系列答案
相关题目
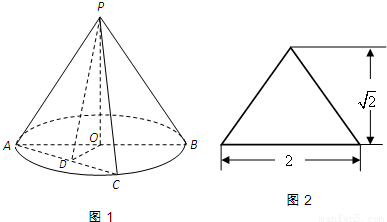
圆锥PO如图1所示，图2是它的正（主）视图．已知圆O的直径为AB，C是圆周上异于A、B的一点，D为AC的中点．
