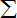题目内容
设 、
、 不共线,点P在AB上,求证:
不共线,点P在AB上,求证: =λ
=λ +μ
+μ 且λ+μ=1,λ、μ∈R.
且λ+μ=1,λ、μ∈R.
证明:∵P在AB上,∴ 与
与 共线.
共线.
∴ =t
=t .∴
.∴ -
- =t(
=t( -
- ).
).
∴ =
= +t
+t -t
-t =(1-t)
=(1-t) +t
+t .
.
设1-t=λ,t=μ,则 =λ
=λ +μ
+μ 且λ+μ=1,λ、μ∈R.
且λ+μ=1,λ、μ∈R.
分析:∵点P在AB上,可知 与
与 共线,得
共线,得 .再用以O为起点的向量表示.
.再用以O为起点的向量表示.
点评:本例的重点是考查平面向量的基本定理,及对共线向量的理解及应用.
 与
与 共线.
共线.∴
 =t
=t .∴
.∴ -
- =t(
=t( -
- ).
).∴
 =
= +t
+t -t
-t =(1-t)
=(1-t) +t
+t .
.设1-t=λ,t=μ,则
 =λ
=λ +μ
+μ 且λ+μ=1,λ、μ∈R.
且λ+μ=1,λ、μ∈R.分析:∵点P在AB上,可知
 与
与 共线,得
共线,得 .再用以O为起点的向量表示.
.再用以O为起点的向量表示.点评:本例的重点是考查平面向量的基本定理,及对共线向量的理解及应用.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目

 、
、 ,设
,设 ,
, ,直线
,直线 上有不同于
上有不同于 (即P分
(即P分 之比为l
).
之比为l
). .
.
 、
、 ,设
,设 ,
, ,直线
,直线 上有不同于
上有不同于 (即P分
(即P分 之比为l
).
之比为l
). .
.